Basic Concepts of Circle

 

Table of Content

What do we mean by the locus of a point? What is a Circle? Perimeter of the Circle Equation of a circle under Different Conditions Parametric Equation of a circle Diameter of circle General equation of a circle in polar co-ordinate system Particular cases of the general equation in polar coordinates Director Circle The Position of a Point with respect to a Circle Related Resources

 

What do we mean by the locus of a point?

Locus of a point is defined to be the path of a point satisfying some geometrical condition; i.e. constraint equations. The path represents a curve, which includes all the points satisfying the given condition.
 

What is a Circle?

A circle is defined as the locus of a point which moves in such a way that its distance from a fixed point is always constant and positive. The fixed point is called the centre of the circle and the given distance the radius of the circle. 

For eg: In real life, when you rotate a stone tied with one end of a string then the path followed by stone is exactly a circle whose centre is your finger an radius is length of the string. 

The equation of a circle with its centre at C(x_c, y_c) and radius r is: 

(x – x_c)² + (y – y_c)² = r² 

Proof: 

Let P(x, y) be any point on the circle. Then by the definition of the locus the constant distance is (see figure given below) 

|PC| = r ⇒ √(x-x_c)² + (y-y_c))²= r 
⇒ (x – x_c)² + (y – y_c)² = r² 

which is the required equation of the circle.

Remark: 
(1) If x_c = y_c = 0 (i.e. the centre of the circle is at origin) then equation of the circle reduce to x² + y² = r². 

(2) If r = 0 then the circle represents a point or a point circle. 
 

Perimeter of the Circle

The perimeter of any figure refers to the sum of the boundaries. Similarly, in case of a circle, the perimeter is given by the circumference of the circle.  

Equation of the circle in Various Forms 

(i) The simplest equations of the circle is x² + y² = r² whose centre is (0, 0) and radius ‘r’. 

(ii) The equation (x – a)²+ (y – b)² = r² represents a circle with centre (a, b) and radius r. 

(iii) The equation x² + y² + 2gx + 2fy + c = 0 is the general equation of a circle with centre (–g, –f) and radius √(g²+f²-c). 

(iv) Equation of the circle with points P(x₁, y₁) and Q(x₂, y₂) as extremities of a diameter is (x – x₁) (x – x₂) + (y – y₁)(y – y₂) = 0.
 

Equation of a circle under Different Conditions

Parametric Equation of a circle 

Let us consider a circle of radius ‘r’ and centre at C(x_c, y_c) we have: 

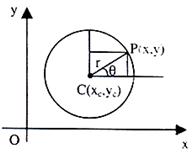(y-y_c)/r = sin θ (see figure given below) 

⇒ y = y_c + r sin θ 

Similarly x = x_c + r cos θ 

This gives the parametric form of the equation of a circle. 
 

Diameter of circle

The locus of middle points of a system of parallel chords of a circle is called the diameter of the circle. The diameter of the circle x² + y² = r² corresponding to the system of parallel chords y = mx + c is x + my = 0.

(a) Every diameter passes through the centre of the circle.

(b) A diameter is perpendicular to the system of parallel chords.
 

General equation of a circle in polar co-ordinate system

Let O be the origin, or pole, OX the initial line, C the centre and ‘a’ the radius of the circle. 

Let the polar co-ordinates of C be R and α, so that OC = R and ∠XOC = α. 

Let a radius vector through O at an angle θ with the initial line cut the circle at P and Q. Let OP be r.

Then we have 

CP² = OC² + OP² – 2OC . OP cos COP 

i.e. a² = R² + r² – 2 Rr cos (θ – α) 

i.e. r² – 2 Rr cos (θ – α) + R² – a² = 0    …… (1) 

This is the required polar equation.
 

Particular cases of the general equation in polar coordinates

1.  Let the initial line be taken to go through the centre C. Then α = 0, and the equation becomes 

r² – 2Rr cos θ + R² – a² = 0. 

2.  Let the pole O be taken on the circle, so that R = OC = α 

The general equation the becomes 

r² – 2ar cos (θ – α) = 0, 

i.e. r = 2a cos (θ – α). 

3. Let the pole be on the circle and also let the initial line pass through the centre of the circle. In this case 

α = 0, and R = a 

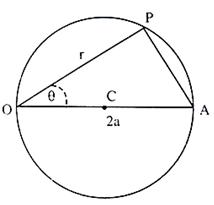Now, the general equation reduces to the simple form r = 2a cos θ 

This is at once evident from the figure given above. 

For, if OCA were a diameter, we have 

OP = OA cos θ, 

r = 2a cos θ. 

Remark: 

∠PRQ = π/2 (Angle subtended by diameter at any point on the circle is a right angle). 

⇒ QR ⊥ PR 

⇒ (Slope of QR) x (Slope of PR) = –1 

⇒ (y-y₂)/(x-x₂) ×(y-y₁)/(x-x₁) = – 1 

⇒ (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0 

which gives the required equation.

Note: 

This equation can also be obtained considering 

PR² + QR² = PQ² 
The general from of the equation of a circle is: 
x² + y² + 2gx + 2fy + c = 0        …… (1) 
⇒ (x + g)² + (y + f)² = g² + f² – c 
Comparing this equation with the standard equation (x – x_c)² + (y – y_c)²= r² 

We have: 

Centre of the circle is (–g, –f), Radius = √(g²+f²-c). 
Equation (1) is also written as S = 0.

Remark: 

1. If g² + f² – c > 0, circle is real 

2. If g² + f² – c = 0, circle is a point circle.

3. If g² + f² – c < 0, the circle is imaginary. 

4. Any second-degree equation ax² + 2hxy + by² + 2gx + 2fy + c = 0 represents a circle only when h = 0 and a = b i.e. if there is no term containing xy and co-efficient of x² and y² are same, provided abc + 2fgh – af² – bg² – ch² ≠ 0
 

Director Circle

The locus of the point of intersection of two perpendicular tangents to a circle is called the director circle. 

We now try to find out the equation of director circle:

If the equation of the circle is x² + y² = a², then the equation of pair of tangents to a circle from a point (x₁, y₁) is 

(x² + y² –a²) (x₁² + y₁² – a²) = (xx₁ + yy₁ – a²)²

If this represents a pair of perpendicular lines then the coefficient of x² + coefficient of y² = 0

i.e. (x₁² + y₁² – a² - x₁²) + (x₁² + y₁² – a² - y₁²) = 0

This gives x₁² + y₁² = 2a²

Hence, this means that the equation of director circle is x² + y² = 2a²

Remark: 

1. Director Circle is a concentric circle whose radius is √2 times the radius of the given circle.

2. The director circle of circle x² + y² + 2gx + 2fy + c = 0 is x² + y² + 2gx + 2fy + 2c - g² - f² = 0.

Illustration: 

Find the centre and the radius 3x² + 3y² – 8x – 10y + 3 = 0. 

Solution: 

We write the given equation as x² + y² – 8/3 x – 10/3 y + 1 = 0. 

⇒ g = -4/3, f = -5/3 , c = 1 

Hence the centre is (4/3,5/3) and the radius is 

√(16/9+25/9-1)=√(32/9)=(4√2)/3.

Illustration: 

Find the length of intercept on y-axis, by a circle whose diameter is the line joining the points (-4, 3) and (12, -1).

Solution: 

The equation of the required circle is (x+4)(x-12) + (y-3)(y+1) = 0

This gives the eqaution as x² + y² – 8x – 2y -51= 0. 

Hence intercept on y-axis is 2√f²-c = 2√(1-(-51)) = 4√13.

Illustration: 

A circle has radius 3 units and its centre lies on the line y = x – 1. Find the equation of the circle if it passes through (7, 3).

Solution: 

Let the centre of the circle be (α, β). It lies on the line y = x – 1 

⇒ β = α – 1. Hence the centre is (α, α – 1). 

⇒ The equation of the circle is (x – α)² + (y – α + 1)² = 9. It passes through (7, 3) 

⇒ (7 – α)² + (4 – α)² = 9 ⇒ 2α² – 22α + 56 = 0 

⇒ α² – 11α + 28 = 0 ⇒ (α – 7) = 0 ⇒ α = 4, 7. 

Hence the required equations are 

x² + y² – 8x – 6y + 6 = 0 and x² + y² – 14x – 12y + 76 = 0.

Illustration: 

Find the equation of the circle whose diameter is the line joining  the points (–4, 3) and (12, –1). Find also the intercept made by it on  the y-axis. 

Solution: 

The equation of the required circle is 

(x + 4) (x – 12) + (y – 3) (y + 1) = 0. 

On the y-axis, x = 0 ⇒ – 48 + y² – 2y – 3 = 0. 

⇒ y² – 2y – 51 = 0 ⇒ y = 1 ± √52. 

Hence the intercept on the y-axis = 22√52 = 4√13.

Illustration: 

Find the equation of the circle passing through (1, 1), (2, –1) and (3, 2). 

Solution: 

Let the equation be x² + y² + 2gx + 2fy + c = 0. 

Substituting the coordinates of three points, we get 
2g + 2f + c = –2, 
4g – 2f + c = –5, 
6g + 4f + c = –13. 
Solving the above three equations, we obtain: 
f = –1/2; g = –5/2, c = 4. 
Hence the equation of the circle is 
x² + y² – 5x – y + 4 = 0.

Illustration: 

Write general equation of a circle centered at a point on x-axis.

Solution: 

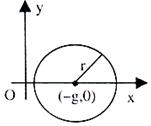Circle is: x² + y² + 2gx + c = 0, g² – c ≥ 0 
Its centre is (–g, 0) and radius √(g²-c) 
Or 
(x + g)² + (y – 0)² = r² 

Its centre is (–g, 0) and radius r. (figure given above) 

Illustration:  

Write the equation of a circle passing through O (0, 0) A (a, 0) and B (0, b)? Obviously AB is the diameter of the circle. (Figure given below) 

Solution: 

Since the circle passes through O (0, 0) A (a, 0) and B (0, b), hence we have the equation as 

(x – a) (x – 0) + (y – 0) (y – b) = 0

Illustration: 

Find the equation of circle shown in figure given below in polar form.

Solution: 

Clearly, OC is the radius. Hence, we have OP = OA cos θ.

This means r = 2a cos θ, – θ/2 ≤ θ ≤ θ/2, where a is radius of circle.

Illustration: 

Find the co-ordinates of the centre of the circle represented by r = A cos θ + B sin θ. 

Solution: 

r = A cos θ + B sin θ 

= [A/√(A²+B² ) cos θ +B/√(A²+B² ) sin θ ] √(A²+B² ) 

= cos (θ – α) (√(A²+B² )) 

centre is ≡ (1/2 √(A²+B² ),tan_-1 (B/A) )

Note: 

1. The equation of the circle through three non-collinear points 

2. The circle x² + y² + 2gx + 2fy + c = 0 makes an intercept on x-axis if x² + 2gx + c = 0 has real roots i.e. if g² > c. And, the magnitude of the intercept is 2√(g²-c). 
 

The Position of a Point with respect to a Circle 

The point P(x₁, y₁) lies outside, on, or inside a circle S ≡ x² + y² + 2gx + 2fy + c = 0, according as S₁ ≡ x₁² + y₁² + 2gx₁ + 2fy₁ + c is greater than, equal to or less than 0.

S₁ > 0 ⇒ Point is outside the circle

S₁ = 0 ⇒ Point is on the circle

S₁ < 0 ⇒ Point is inside the circle
 

Related Resources

• Click here to refer the most Useful Books of Mathematics.

• For getting an idea of the type of questions asked, refer the previous year papers.

• Fast Track your revision with the ultimate Revision Notes on Circle.

To read more, Buy study materials of Circles comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.