Objective Type Questions

            at x = –2         local minima

                x = 0            local maxima

                x = 2            local minima

45. Let f (x) = x³ – 6x² + 9x + 18, then f (x) is strictly decreasing in

            (A) (–∞, 1]                                             (B) [3, ∞)

            (C) (–∞, 1] U [3, ∞)                                 (D) [1, 3]               

Solution: 

(D)       f(x) = x³ – 6x² + 9x + 18

            f'(x) = 3x² – 12x + 9

                   = 3(x² – 4x + 3)

                   = 3(x – 1)(x – 3) £ 0

                x ∈ [1, 3]

46. The absolute minimum value of x⁴ – x² – 2x+ 5

            (A) is equal to 5                                    (B) is equal to 3

            (C) is equal to 7                                    (D) does not exist

Solution: 

(B)       f(x) = x⁴ – x² – 2x + 5

            f'(x) = 4x³ – 2x – 2

                   = (x – 1) (4x² + 4x + 2)

Clearly at x = 1, we will set the minimum value which is 3.

47. Equation of the tangent to the curve y = e^–|x| at the point where it cuts the line x=1

            (A) is ey + x =2                   (B) is x + y = e

            (C) is ex + y = 1                  (D) does not exist

Solution: 

(A) y = e^–|x| cut the line x = 1 at (1, 1/e)

                        (dy/dx)_(11,1/e) = –1/e

            Tangent y = –1/e  = –1/e (x – 1)

            =>        ey + x = 2

48. Rolle’s theorem holds for the function x³ + bx² + cx, 1 < x < 2 at the point 4/3, the value of b and c are;

            (A) b = 8, c = - 5                       (B) b = -5, c = 8   

            (C) b = 5, c = -8                        (D) b = -5, c = -8.

Solution: 

(D)       f'(4/3) = 0

            =>        16 + 8b + 3c = 0

            Also f(1) = f(2)

            =>        3b + c + 7 = 0

            Hence b = – 5, c = –8

49. The number of value of k for which the equation x³ – 3x + k = 0 has two different roots lying in the interval (0, 1) are

            (A) 3                                          (B) 2

            (C) infinitely many                         (D) no value of k satisfies the requirement.

Solution: 

(C)       Let f(x) = x³ – 3x + k

            f'(x) = 3(x – 1) (x + 1)

            only are root may lie between –1 and 1

50. From mean value theorem: f(b) – f(a) = (b –a) f' (x₁); a < x₁ < b if f(x) = 1/x , then x₁ =

            (A) √ab                          (B) a+b/2

            (C) 2ab/q+b                    (D) b–a/b+a

Solution: 

(A)       Since f(x) = 1/x

            f'(x₁) = f(b) – f(a) / b – a

13.1    OBJECTIVE LEVEL – 2

51. The minimum value of ax + by, where xy = r², is (r, ab >0)

            (A) 2r √ab                                (B) 2ab√r

            (C)       –2r √ab                        (D) None of these

Solution: 

(A)       Let f(x) = ax + br² / x 

            f ’(x) = a – br² / x = 0

            x = √b / √a r 

            f (√b / √a r) = a√br / √a + √br² / √br √a = 2r √ab 

52. If a, b, c, d are four positive real numbers such that abcd =1, then minimum value of (1+ a) (1 + b) (1 + c) (1 + d) is

            (A) 8                                    (B) 12

            (C) 16                                   (D) 20

Solution: 

(C)       Applying AM ³GM

Multiplying all focus (1 + a) (1 + b)(1 + c)(1 + d) ³ 16

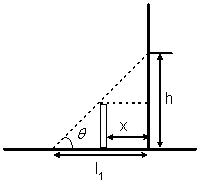
53. A lamp of negligible height is placed on the ground ‘l₁’ metre away from a wall. A man ‘l₂’ metre tall is walking at a speed of l₁/10 m/sec. from the lamp to the nearest point on the wall. When he is mid-way between the lamp and the wall, the rate of change in the length of this shadow on the wall is

            (A) –5l₂ / 2 m/sec.                   (B) –2l₂ / 5 m/sec.

            (C) –l₂ / 2 m/sec.                     (D) –l₂ / 5 m/sec.

Solution: 

(B)       Clearly h / l₁ = l₂ / l₁ – x

            => hl₁ – hx = l₁l₂        (Since h is decreasing put a – ve sign)

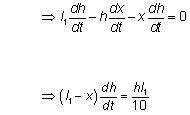
at mid point x₁ = l₁/2, h = 2l₂

=> dh/dt = 2l₂/5 

f ’(x) = 2e^x + ae^-x + 2a + 1> 0 clear a > 0

54. Let f (x) = 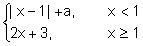. If f (x) has a local minima at x = 1, then

            (A) a > 5                          (B) a > 5

            (C)       a > 0                    (D) none of these

Solution: 

            (A) f (x) =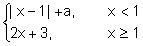 

            Local minimum value of f (x) at x = 1, will be 5

            i.e. 1 –x + a ³ 5 at x = 1 => a ³ 5

55. Global minimum value of f (x) = x⁸ + x⁶ –x⁴ –2x³ –x² –2x + 9 is

            (A) 0                                 (B) 1

            (C) 5                                 (D) 9

Solution: 

(C) We will get the minimum value of f(x) at x = 1 which is 5