Fundamental Principle of Counting
Table of Content |
What is the Fundamental Counting Principle in math?
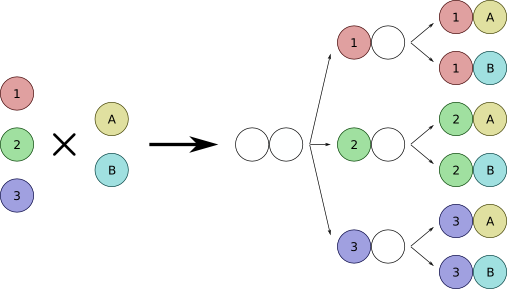
Fundamental counting principle stats that, if we have m ways of doing a task and n ways of performing another task, and if the job or event is said to be completed when both the tasks are done or finished in a definite order then the total number of ways in which the job or event can be done will be equals to m x n ways.
For Example: In an event of eating a complete lunch, if one has 5 choices in starters and 15 options for main course, then the number of ways in which he/she can take his lunch will be = 5 x 15 = 75.
This principle ‘Fundamental principle of counting’ in short FPC is used to count the number ways of successfully performing any task or event without actually counting them.
Let us take the two different models to understand this principle.
Model 1: Find the number of ways of travelling from T1 to T3 via T2,
In this model, assuming we have 3 different means (may be bike, public transport and private transport) for travelling from T1 to T2 and two different ways of travelling from T2 to T3 (may be by train and airways)
So, to count for all the possible ways, we may have,
T1 – R1 – T2 – R4 – T3
T1 – R1 – T2 – R5 – T3
T1 – R2 – T2 – R4 – T3
T1 – R2 – T2 – R5 – T3
T1 – R3 – T2 – R4 – T3
T1 – R3 – T2 – R5 – T3 = 6 ways.
Thus, it can also be seen by careful observation, that we have, 3 different ways to travel from T1 to T2 and 2 for T2 to T3.
Thus, the total ways = 3 x 2 = 6
In General, if we have m ways from T1 to T2 and n ways from T2 to T3. Then the number of ways to travel from T1 to T3 will be equals to m x n.
This concept of counting can also be extended to any number of events. For example, if m1, m2, m3, …... mn are the number of ways of performing different events, then the total number of ways in which all the events can be completed in a definite order will be equals to m1 x m2 x m3 x …… x mn.
Refer the figures below, to have some more examples
Model 2: Let’s see this model on two different conditions.
-
Finding the number of ways to enter and leave the cinema hall by different gate.
In the figure, we have 5 different gates to enter or leave the cinema hall. As per the given conditions, the person is supposed to enter and leave by different gate (same gate should not be used)
Thus, the person has 5 gates to choose from to enter the cinema hall but only 4 gates to choose to come out or leave the hall. The gate though which he/she entered will not be considered while coming out.
Thus, the total number of ways in which one can enter and leave the cinema hall by different gate will be equals to 5 x 4 = 20 ways.
-
Finding the number of ways to enter and leave the cinema hall by any gate.
What is the addition Principle of Counting?
Addition principle of counting gives us the number of possibilities of doing any of the given task from the given different tasks.
If E1 and E2 are two mutually exclusive events i.e. no any common outcomes, then the number of ways of doing the event either E1 or E2 will be equals to m + n, where m and n are the number of ways of doing the events E1 and E2 respectively. This concept can be extended for the any number of events.
For Example: If there exists 5 different medical entrance exams and 10 different engineering entrance exams, then the number of ways in which any student of grade 10th will be appearing in any one of the exam (after 12th) from either medical or engineering will be equals to 5 + 10 = 15.
In this case, we shall have 5 ways to enter and 5 ways to exit the hall. Thus, the total number of ways to enter and leave the cinema hall by any gate will be equals to 5 x 5 = 25.
Give any one practical example of Principle of Counting
Lexicography is the technique or science of making words. Given some combination of letters, and to find its position when arranged in the dictionary order is an example or area where principle of counting is used at most.
This position of any word in a dictionary which is composed of all the words with permutations from given letters is called its rank.
Example: Find the rank of the word ‘VIRAT’ if all the letters are permuted and written in the dictionary format.
Before preceding ahead, this must be noted that, the number of ways of forming 5 lettered words using 5 different letters is = 5 x 4 x 3 x 2 x 1 = 120. Here, 5 is the number of ways of filling first place, 4 is the number of filling second place (given the first place is filled), 3 is the number of filling the third place (given the first and second places are filled) and so on.
To find the rank of the given word ‘VIRAT’ which is composed of V, I, R, A and T. First arrange them in the alphabetical order as – A, I, R, T, V
Number of words beginning with A – 4 x 3 x 2 x 1 = 24 ways
Number of words beginning with I – 4 x 3 x 2 x 1 = 24 ways
Number of words beginning with R – 4 x 3 x 2 x 1 = 24 ways
Number of words beginning with T – 4 x 3 x 2 x 1 = 24 ways
Number of words beginning with VA – 3 x 2 x 1 = 6 ways
Number of words beginning with VIA – 2 x 1 = 2 ways
Next word will be VIRAT = 1 way
Thus, Rank = 24 + 24 + 24 + 24 + 6 + 2 + 1 = 105.
What is a Permutation and a Combination?
These two words Permutation and Combination, at the initial level are very confusing and are generally used interchangeably. So, let’s take them one by one and understand them.
Combination means from the given certain objects (may be alike or different) selecting one or more objects. Combination can also be replaced by the words – selection, collection or committee.
For Example: Combination of top 5 cricket players from the team of 11 players is the selection of 5 players (in any order).
The sequence in which they have to be selected is not important here. Also, we can say that the order of selection is not the concern in the case of combination
The word permutation means arrangement of the alike or different objects taken some or all at a time. So, we can observe the word ‘arrangement’ used in the definition of permutation. Here the arrangement means selection as well as ordering. That means the order in which the objects are selected have also been taken care of in this case.
For Example:The number of 5 digit numbers which can be formed using the digits 0, 1, 2, 3, 4 & 5.
In this example, we just not have to select the 5 digits out of given 6 digits but also have to 21034, 42351 are all different cases.
What is distinguishable permutations?
Distinguishable permutations are the permutations which are different from each other. The number of distinguishable permutations of n things (taken all at a time) out of which – p are all alike and is of one kind, q are also alike but of another kind and rest all different will be given by
For Example: The permutations of the numbers 1, 2 and 3 will be – 123, 132, 213, 231, 312, 321. All these 6 permutations (that is, 3!) are different and thus are distinguishable permutations.
But let us take another example where we have to find the permutations of the numbers 1, 2 and 1 (here we have 2 ones). In this case, the possible permutations will be 121, 112, 211, 211, 121, 112. Again, we have 6 permutations but out of these only 3 are distinguishable or different.
Thus, the number of distinguishable permutations will be calculated as 3!/2! = 3
Let us take one of the favorite example of permutations.
Example: Find the number of different permutations of the word ‘ASSASSINATION’
In this example, we have given 13 alphabets in which A occurs 3 times, S occurs 4 times, I occurs 2 times, N occurs 2 times, T and O occurs 1 times each.
So, the number of different permutations possible = 
IIT JEE study material is available online free of cost at askIITians.com. Study Permutations and Combinations and a number of topics of Algebra at askIITians website and be a winner. We offer numerous live online courses for IIT JEE preparation - you do not need to travel anywhere any longer - just sit at your home and study for IIT JEE live online with askIITians.com
To read more, Buy study materials of Permutations and Combinations comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.
More Readings