Permutations and Combinations
Table of Content |
|
|
What do you mean by Permutation and Combination?
These two words permutation and combination, at the initial level are very confusing and are generally used interchangeably. So let’s take them one by one and understand them.
Combination means from the given certain objects (may be alike or different) selecting one or more objects. Combination can also be replaced by the words – selection, collection or committee.
For Example – Combination of top 5 cricket players from the team of 11 players is the selection of 5 players (in any order).
The sequence in which they have to be selected is not important here. Also we can say that the order of selection is not the concern in the case of combination
The word permutation means arrangement of the alike or different objects taken some or all at a time. So we can observe the word ‘arrangement’ used in the definition of permutation. Here the arrangement means selection as well as ordering. That means the order in which the objects are selected have also been taken care of in this case.
For Example – The number of 5 digit numbers which can be formed using the digits 0, 1, 2, 3, 4 and 5.
In this example, we just not have to select the 5 digits out of given 6 digits but also have to see the number of possible cases for the different arrangement. So the numbers 34251, 21034, 42351 are all different cases.
We will try to explore these definitions in the upcoming heading.
What is Factorial Notation in mathematics?
Since the definition or the formula of both, permutation and combination, requires the use of factorial notation, so let’s first understand this here before learning any further.
In Mathematics, the factorial is represented by the symbol ‘!’ i.e. if we have to write 5 factorial, so it will be written as 5! So in general factorial of any positive number n will be represented by n!.
Mathematically,
where n is any positive integer.
So, 4! = 3! x 4 = 2! x 3 x 4 = 1! x 2 x 3 x 4 = 0! x 1 x 2 x 3 x 4 = 1 x 2 x 3 x 4
Similarly we can say for any positive integer ‘n’
n! = n x (n – 1) x (n – 2) x …….. x 3 x 2 x 1.
Thus, we seeing the above equation, we may also define the factorial of any positive integer n as ‘the product of all the positive integers less than or equal to n’.
Just see below for the factorial of few frequently used numbers.
0! = 1
2! = 2 x 1 = 2
3! = 3 x 2 x 1 = 6
4! = 4 x 3 x 2 x 1 = 24
5! = 5 x 4 x 3 x 2 x 1 = 120 and so on.
Differentiate Permutation and Combination
The very basic difference in permutation and combination is the order of the objects considered. In combination, the order is not considered at all while for permutation it is must. So the permutation is the ordered arrangement while the combination is the unordered selection.
From the three alphabets A, B and C, the permutation of these 3 letters will be ABC, ACB, BAC, BCA, CBA and CAB. While the combination of 3 letters will be just (A, B, C).
Permutation gives the answer to the number of arrangements while the combination explains the possible number of selections.
Permutation of a single combination can be multiple but the combination of a single permutation is unique (considering all at a time).
Explain Permutation with some practical examples
Permutation refers to the situation where the arrangement of objects are being considered.
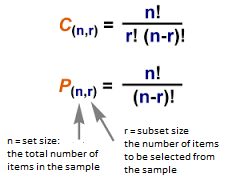
In general, the permutation of n distinct objects taken r at a time, is represented and calculated as:
This can also be represented as P(n, r) or Pnr. Here, in the definition of permutation, r can be any positive integer less then or equals to n. So on the basis of the values of r whether it is less then or equals to n we can have two different conditions or theorems.
Theorem – 1
The number of permutations or arrangement of n distinct things taken all at a time can be represented by:
Example
Consider the 5 seats in a car on which 5 persons are to be seated.
So to find the number of cases in which 5 persons can be seated will be the case of permutation of 5 persons taking all 5 seats at a time (5P5).
Theorem - 2
The number of permutations or arrangement of n distinct things taken only r (r < n) at a time can be represented by:
Example
Consider the 10 chairs in a room for which 15 persons are supposed to be seated.
In this case, here we have 15 persons to be arranged but only on 10 chairs. So this can be calculated by15P10.
One more thing which we can learn by observing the above example is that, we first need to choose or select 10 out of 15 persons which can be arranged on 10 available chairs.
So, every problem on permutation is broken down into selection and then arrangement.
that is, Permutation = Selection x Arrangement
What do you mean by Combination? Give some examples
Combination is the selection or collection of one or more things from the given list of alike or distinct objects taken all or some at a time.
In general, the combination of n distinct objects taken r at a time, is represented and calculated as:
This can also be represented as 
Here, in the definition of combination, r can be any positive integer less then or equals to n.
Let’s discuss few important cases here in combination.
Theorem - III
The number of combination of n different things taken r at a time.
Example
Calculate the number of selections of 3 different colored pens from the available 5 pens of all different colored pens
Here, we just need to select 3 pens (in any order) from the available 5 pens. This can be calculated as:
Here, in this theorem, note that if r = n that is, all the things have to be selected.
So,
, which is very obvious.
Theorem – IV
Number of combination of n different things taken r at a time when p particular things are always included will be calculated as
n-pCr-p
Example
Calculate the number of ways of combination or selection of 11 players out of 20 players when virat kohli, M.S. Dhoni and Y. Singh are always included.
Here we have been giving 20 players of which only 11 players are to be selected. We are also given the 3 players out of 20 which must be included in any case. So actually we can understand that, out of 11 we have already 3 players so we just need to select 8 addition players from the remaining 17 players.
Thus, Total number of ways for the above problem = 20-3 C11-3 = 17C8
Theorem - V
The number of combination of n different things taken r at a time when p particular things are always excluded can be calculated as:
n-pCr
Let’s take the same kind of example which we have discussed in previous theorem.
Example
Calculate the number of ways of combination or selection of 11 players out of 20 players ravindra jadeja and balaji are always excluded.
Again we have been given 20 players of which 11 players to be selected but this time 2 specific players are to be excluded. Thus actually we have the option of 18 players effectively for selecting 11 players.
Thus, The total number of selections = 20-2C11 = 18C11
Is there any relation between Permutation and Combination?
As discussed in the previous sections, permutation is the combination (or selection) and the arrangement as well.
Thus, while calculating the permutation, we first need to choose or selecting the thing before their arrangement.
So,
Permutation = Selection x Arrangement
This can also be understood from their mathematical relation. Since we know that,
Thus, from the above two formulas, this is very clear that
nPr = nCr r!
where, nCr denotes the selection and r! denotes the arrangement of r objects for the r places.
Watch this Video for more reference
Related Resources
-
Click here for the Complete Syllabus of IIT JEE Mathematics..
-
Look into the Past Year Papers with Solutions to get a hint of the kinds of questions asked in the exam.
-
You can get the knowledge of Useful Books of Mathematics here.
To read more, Buy study materials of Permutations and Combinations comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.
More Readings