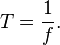Ask a Doubt
Get your questions answered by the expert for free
Enter text here...
Other Related Questions on wave optics

An oscillator consists of a block of mass 512 g connected to a spring. When set into oscillation with amplitude 34.7 cm, it is observed to repeat its motion every 0.484 s. Find (a) the period, (b) the frequency, (c) the angular frequency, (d) the force constant, (e) the maximum speed, and ( f ) the maximum force exerted on the block.
wave optics
0 Answer Available
Last Activity: 2 Years ago

A PLANE TRANSMISSION GRATING HAS 45000 LINES. DETERMINE ITS RESOLVING POWER IN THE SECOND ORDER FOR WAVELENGTH OF 5000A.
wave optics
0 Answer Available
Last Activity: 3 Years ago

A PLANE TRANSMISSION GRATING HAS 45000 LINES. DETERMINE ITS RESOLVING POWER IN THE SECOND ORDER FOR WAVELENGTH OF 5000A.
wave optics
0 Answer Available
Last Activity: 3 Years ago

If V-numer of a multi mode fiber is 3. Calculate the no.of modes if it is step index and graded index fiber multimode fiber (rounded off)?
wave optics
1 Answer Available
Last Activity: 3 Years ago

What is the difference between angular position and angular fringe width... I always get confused .
wave optics
2 Answers Available
Last Activity: 3 Years ago