explain differential equation behind wave motion.

Mathematically, the most basic wave is the sine wave (or harmonic wave or sinusoid), with an amplitude u described by the equation:

where A is the semi-amplitude of the wave, half the peak-to-peak amplitude, often called simply the amplitude – the maximum distance from the highest point of the disturbance in the medium (the crest) to the equilibrium point during one wave cycle. In the illustration to the right, this is the maximum vertical distance between the baseline and the wave; x is the space coordinate, t is the time coordinate, k is the wavenumber (spatial frequency), ω is the temporal frequency, and φ is a phase offset.

The wave equation

The wave equation is a partial differential equation that describes the evolution of a wave over time in a medium where the wave propagates at the same speed independent of wavelength , and independent of amplitude .

consider the wave equation in one dimension, for example, as applied to a string. Suppose a one-dimensional wave is traveling along the x axis with velocity v and amplitude u (which generally depends on both x and t), the wave equation is

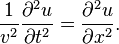
The velocity v will depend on the medium through which the wave is moving.

The general solution for the wave equation 

This formula represents two shapes traveling through the medium in opposite directions; F in the positive x direction, and G in the negative x direction, of arbitrary functional shapes F and G.

--

regards

Ramesh