Hi,
In calculus, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much a quantity is changing at a given point; for example, the derivative of the position (or distance) of a vehicle with respect to time is the instantaneous velocity (respectively, instantaneous speed) at which the vehicle is traveling. 

For a real-valued function of a single real variable, the derivative at a point equals the slope of the tangent line to the graph of the function at that point. 

The process of finding a derivative is called differentiation. The fundamental theorem of calculus states that differentiation is the reverse process to integration.
Differentiation is a method to compute the rate at which a dependent output y changes with respect to the change in the independent input x. This rate of change is called the derivative of y with respect to x. In more precise language, the dependence of y upon x means that y is a function of x. If x and y are real numbers, and if the graph of y is plotted against x, the derivative measures the slope of this graph at each point. This functional relationship is often denoted y = ƒ(x), where ƒ denotes the function.
The simplest case is when y is a linear of x, meaning that the graph of y against x is a straight line. In this case, y = ƒ(x) = m x + c, for real numbers m and c, and the slope m is given by

where the symbol Δ (the uppercase form of the Greek letter Delta) is an abbreviation for "change in." This formula is true because
y + Δy = ƒ(x+ Δx) = m (x + Δx) + c = m x + c + m Δx = y + mΔx.
It follows that Δy = m Δx.
This gives an exact value for the slope of a straight line. If the function ƒ is not linear (i.e. its graph is not a straight line), however, then the change in y divided by the change in x varies: differentiation is a method to find an exact value for this rate of change at any given value of x.
Rate of change as a limiting value


The tangent line at (x, ƒ(x))




such an infinitesimal change in x is denoted by dx, and the derivative of y with respect to x is written 

suggesting the ratio of two infinitesimal quantities.

The secant to curve y= ƒ(x) determined by points (x, ƒ(x)) and (x+h, ƒ(x+h))


The tangent line as limit of secants


the difference between the x values, that is, 

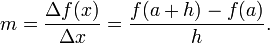
The derivative is the value of the difference quotient as the secant lines approach the tangent line. Formally, the derivative of the function ƒ at a is the limit

of the difference quotient as h approaches zero, if this limit exists. If the limit exists, then ƒ is differentiable at a. Here f′ (a) is one of several common notations for the derivative 
 
Regards,
Rajat
Askiitian Expert