Hello student,
First of all, select two arbitrary points P
1(x
1, y
1, z
1) and P
2(x
2, y
2, z
2) on
Ax + By + Cz + D
1 = 0 and Ax + By + Cz + D
2 = 0 respectively.
Now, therefore, the vector t = <x
2-x
1, y
2-y
1, z
2-z
1> is the vector starting at P
1 and ending at P
2.
Moreover, the projection of vector t onto the normal vector n = <a, b, c> is the distance between the two planes.
This length will therefore be given by the modulus of the projection of t onto n and is therefore given as under:
Now, since the points lie on the given planes so we have
Ax
1 + By
1 + Cz
1 = -D
1 and Ax
2 + By
2 + Cz
2 = -D
2.
Hence, using these the above expression reduces to
This is the required formula.
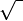A^2+B^2+C^2
