1800-150-456-789
FlagBACK
Flag Thermal Physics> Please tell above answer quickly and as s...
question mark

Please tell above answer quickly and as soon as possible........................

Anvita Mahajan , 5 Years ago
Grade
anser 1 Answers
Samyak Jain

Last Activity: 5 Years ago

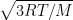
RMS speed of ideal gas molecules is \sqrt{3RT/M} , where T is the temperature in kelvin, R is universal gas constant,
M is the molar mass of gas.
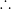
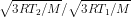
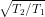
\therefore ratio of rms speeds of molecules at T2 and T1 is \sqrt{3RT_2 / M} / \sqrt{3RT_1 / M} = \sqrt{T_2 / T_1}  …..(1)
Now, we need to compute temperatures T1 and T2.
We know that for isotherm, PV = constant i.e. PV = nRT and T is constant.
Consider isotherm at T1. It is passing through P = 1.105 Pa and V = 1 m3.
So, 1.105 Pa . 1 m3 = nR T1  or  T1 = (105 / nR) K
Similarly, for T2, P = 2.105 Pa and V = 2 m3.
So, 2.105 Pa . 2 m3 = nR T2  or  T2 = (4.105 / nR) K
Substitute value of T1 and T2 in (1) and you will get
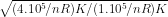
ratio of rms speeds = \sqrt{(4.10^5 / nR) K / (1.10^5 / nR) K}   =  2 .

Provide a better Answer & Earn Cool Goodies

Enter text here...
star
LIVE ONLINE CLASSES

Prepraring for the competition made easy just by live online class.

tv

Full Live Access

material

Study Material

removal

Live Doubts Solving

assignment

Daily Class Assignments


Ask a Doubt

Get your questions answered by the expert for free

Enter text here...

Other Related Questions on Thermal Physics

question mark
A container filled with a sample of an Idea gas at the pressure of 1.5atm. the gas is compressed isothermal ly to one fourth of its original volume. What is the new pressure of the gas?
Thermal Physics
0 Answer Available

Last Activity: 1 Year ago(s)

question mark
how do we know the electric field due to an electric dipole of dipole moment P at distance r from the centre of dipole is fiven by .. where theta is angle between p amd r vector..
Thermal Physics
0 Answer Available

Last Activity: 2 Year ago(s)

question mark
A A mole of helium gas initially at stp undergoes an isovolumetric process in which its pressure falls to half its initial value. The work done by gas is
Thermal Physics
0 Answer Available

Last Activity: 2 Year ago(s)

question mark
\t5000 J of heat are added to two moles of an ideal monatomic gas, initially at a temperature of 500 K, while the gas performs 7500 J of work. What is the final temperature of the gas? step by step please
Thermal Physics
1 Answer Available

Last Activity: 2 Year ago(s)

question mark
Please help me with theanswer of this questionrelated to radiation graph
Thermal Physics
0 Answer Available

Last Activity: 2 Year ago(s)