Thermal Physics> a pendulum clock becomes 5sec fast each d...

a pendulum clock becomes 5sec fast each day at temp at 15 c and becomes 10 sec slow each day at temp 30 c .the temp at which the clock gives correct time is

sandhya , 8 Years ago

Grade 12th pass

4 Answers

arun

Last Activity: 8 Years ago

in this we have to use mainly three concepts which are L₂=L₁(1+(alpha)(change in temprature))

another is binomial theorem which is (1 + x )ⁿ= 1 + nx for x

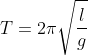
and the last one which is $T = 2\pi\sqrt{\frac{l}{g}}$

now it is given that clock is 5 seconds fast each day i.e. 1.16 $\times$ 10^-4seconds

i.e. time period at that temprature is (2 – 1.16 $\times$ 10^-4)

and let at $\theta$ temprature it shows correct time i.e. it’s time period is 2 seconds

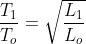
now, $\frac{T_{1}}{T_{o}}=\sqrt{\frac{L_{1}}{L_{o}}}$

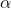
and L₁ = L_o(1 + $\alpha$ (15 – $\theta$ ))

$\Rightarrow \frac{T_{1}}{T_{o}}=\sqrt{\frac{L_{o}(1 + \alpha (15 - \theta ))}{L_{o}}}$

using binomial theorem

$\Rightarrow \frac{T_{1}}{T_{o}}=1 - \frac{1}{2}\alpha(15 - \theta )$

$\frac{2 - 1.16 \times 10^{-4}}{2} = 1 + \frac{1}{2}\alpha (\theta - 15)$

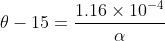
$\theta - 15 = \frac{1.16 \times 10^{-4}}{\alpha}$ …......................1

similarly

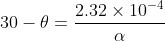
$30 - \theta = \frac{2.32 \times 10^{-4}}{\alpha}$ …............................2

now subtracting adding equation 1 and 2 we get

$15 = \frac{3.48 \times 10^{-4}}{\alpha}$

$\Rightarrow \alpha = \frac{3.48 \times 10^{-4}}{15}$

substituting it in equation 1 we get

$\theta - 15 = 5$

$\Rightarrow \theta = 20$

so clock will give correct time at 20 ^oC

Sandesh

Last Activity: 7 Years ago

A simple method to solve this is the following:Time lost or gained= aplha∆t/2 X given time periodCase 1: Time gained is 5s so the condition is like this: 5=alpha(t-15)/2 where it`s (t-15) as it`s gained so t is at more temp.Case 2: Time lost is 10s so the condition is like this: 10=alpha(30-t)/2 where it`s (30-t) as it`s lost so t is at a less temp.Dividing these two equations we get the temp at which clock gives correct time.10/5=(30-t)/2 X 2/(t-15)2(t-15)=30-t2t-30=30-t3t=60T=20°