The system shown in figure is released from rest at t=0. Block A hits the pulley at t=x and B hits the at t=y. If pulley and strings are ideal the find the ratio of x and y .

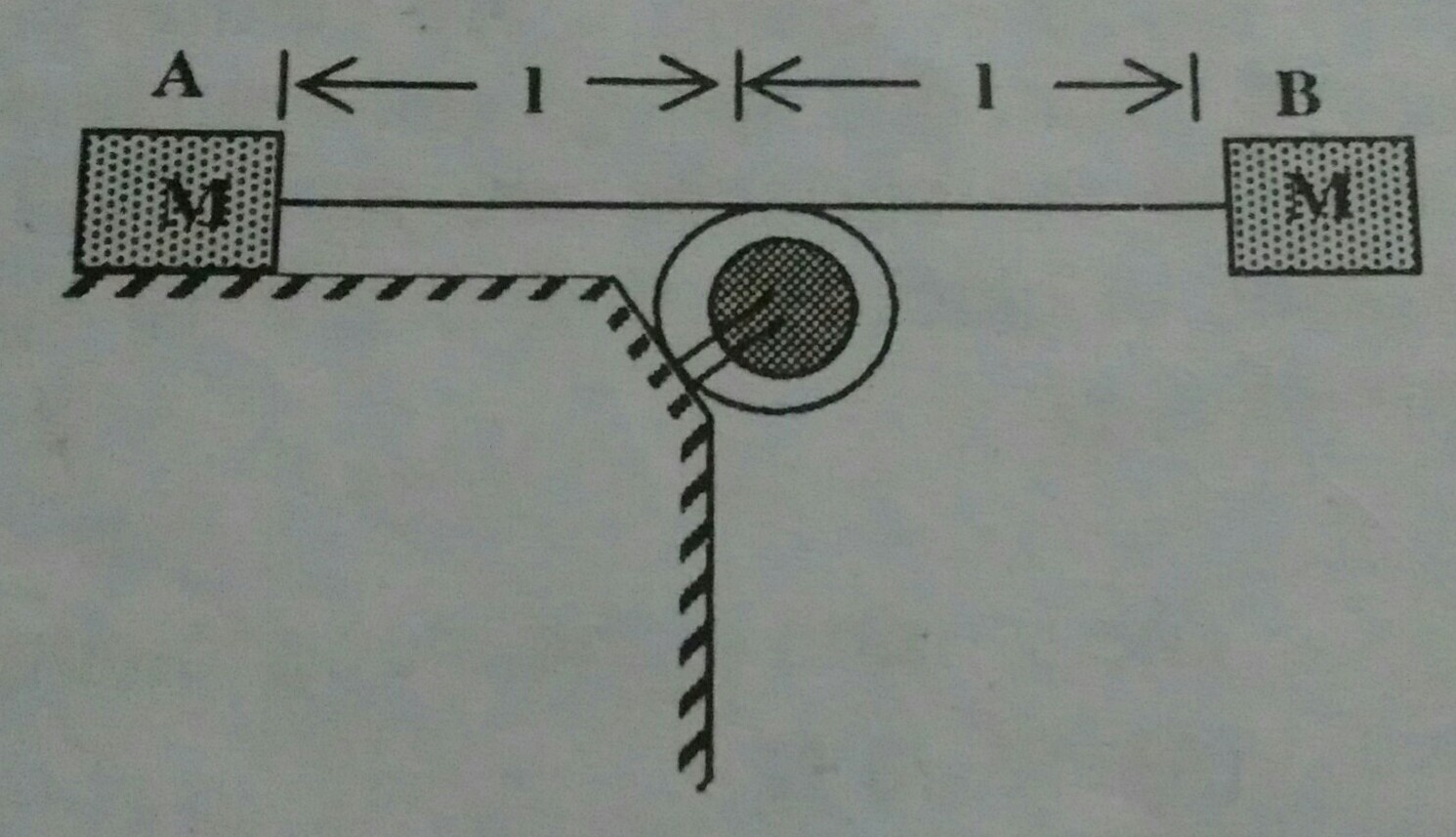
To solve the problem of finding the ratio of the times $x$ and $y$ when blocks A and B hit the pulley, we need to analyze the motion of both blocks under the influence of gravity. Let's assume that block A is hanging on one side of the pulley and block B is on the other side, with both blocks having the same mass $m$. The system is released from rest, meaning both blocks start with an initial velocity of zero.

Understanding the Motion of the Blocks

When the system is released, both blocks will accelerate due to gravity. The key to solving this problem lies in understanding how far each block travels before they hit the pulley.

Acceleration of the Blocks

Since the pulley and strings are ideal (massless and frictionless), the only force acting on each block is its weight. The acceleration $a$ of each block can be expressed as:

• For block A (going down): $F=m\cdot g$ (downward force)
• For block B (going up): $F=m\cdot g$ (upward force)

Since both blocks are connected by a string over the pulley, they will have the same magnitude of acceleration, which is given by:

a = g

Distance Travelled by Each Block

Let’s denote the distance travelled by block A before it hits the pulley as $d_A$ and the distance travelled by block B as $d_B$. Since both blocks are released from rest, we can use the equation of motion:

d = \frac{1}{2} a t^2

For block A, the distance travelled before hitting the pulley is:

d_A = \frac{1}{2} g x^2

For block B, the distance travelled before hitting the pulley is:

d_B = \frac{1}{2} g y^2

Setting Up the Ratio

Since the distances $d_A$ and $d_B$ are equal when both blocks hit the pulley, we can set the two equations equal to each other:

$\frac{1}{2}g{x}^2=\frac{1}{2}g{y}^2$

We can simplify this equation by canceling out the common factors:

x^2 = y^2

Taking the square root of both sides gives us:

x = y

Final Ratio

Thus, the ratio of the times at which blocks A and B hit the pulley is:

$\frac{x}{y}=1$

This means that both blocks hit the pulley at the same time, indicating that they travel equal distances in the same amount of time due to their equal masses and the symmetry of the system. This result is a direct consequence of the ideal conditions assumed in the problem.