The block of mass m is slightly displaced from equilibrium position and then released in the system as shown. Find the period pf the vertical oscillations. The pulleys are massless and frictionless.

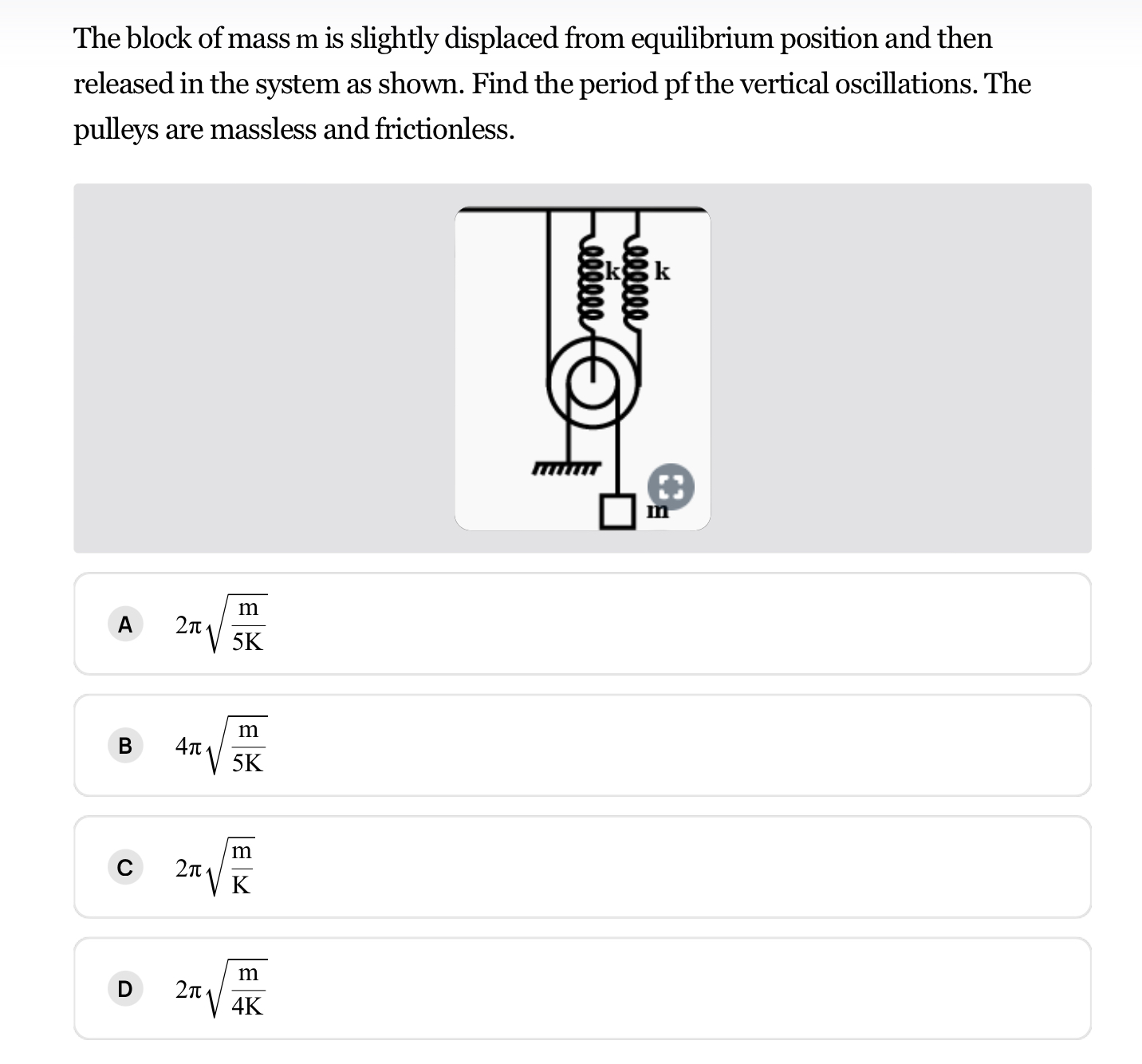
To determine the period of vertical oscillations for the block of mass \( m \) in the described system, we can analyze the forces acting on the block and apply the principles of simple harmonic motion (SHM). The setup likely involves a mass hanging from a pulley system, which can be modeled as a spring-mass system when displaced slightly from its equilibrium position.

Understanding the Forces at Play

When the block is displaced slightly from its equilibrium position and released, it experiences a restoring force due to gravity. This force will pull the block back toward its equilibrium position, causing it to oscillate. The key to finding the period of these oscillations lies in understanding the relationship between the restoring force and the displacement from equilibrium.

Applying Newton's Second Law

Let’s denote the displacement from the equilibrium position as \( y \). The gravitational force acting on the block is \( F_g = mg \), where \( g \) is the acceleration due to gravity. When the block is displaced by a small distance \( y \), the net force acting on it can be expressed as:

• The restoring force due to gravity: \( F_{restoring} = -mg \) (acting downward when displaced upward).

According to Newton's second law, the net force is also equal to the mass times acceleration:

\( F_{net} = ma = m \frac{d^2y}{dt^2} \)

Setting these two expressions for force equal gives us:

\( m \frac{d^2y}{dt^2} = -mg \)

Dividing through by \( m \) (assuming \( m \neq 0 \)) leads to:

\( \frac{d^2y}{dt^2} = -g \)

Identifying Simple Harmonic Motion

This equation resembles the standard form of SHM, which is:

\( \frac{d^2y}{dt^2} = -\omega^2 y \)

Here, \( \omega \) is the angular frequency of the oscillation. By comparing the two equations, we can see that:

\( \omega^2 = \frac{g}{L} \)

where \( L \) is the effective length of the system (which may depend on the configuration of the pulleys and the mass). The period \( T \) of the oscillation can be derived from the angular frequency using the relationship:

\( T = 2\pi \sqrt{\frac{L}{g}} \)

Finalizing the Period Calculation

To summarize, the period of the vertical oscillations of the block is given by:

\( T = 2\pi \sqrt{\frac{L}{g}} \)

In this formula, \( L \) represents the effective length from the pivot point of the pulley to the center of mass of the block. If the system has multiple pulleys or additional complexities, you may need to adjust \( L \) accordingly. However, for a simple setup with one mass hanging directly from a pulley, this formula will provide the correct period of oscillation.

In practical terms, if you were to measure the time it takes for the block to complete one full oscillation (down and back up), you would find that it aligns with this calculated period. This relationship between mass, gravity, and oscillation period is fundamental in understanding systems that exhibit harmonic motion.