Sir please explain this Q again bcz I was unable to understand it.What is line of impact here,and from where vcostheta come,why e=tan²theta,pls pls pls clear this Q to me.

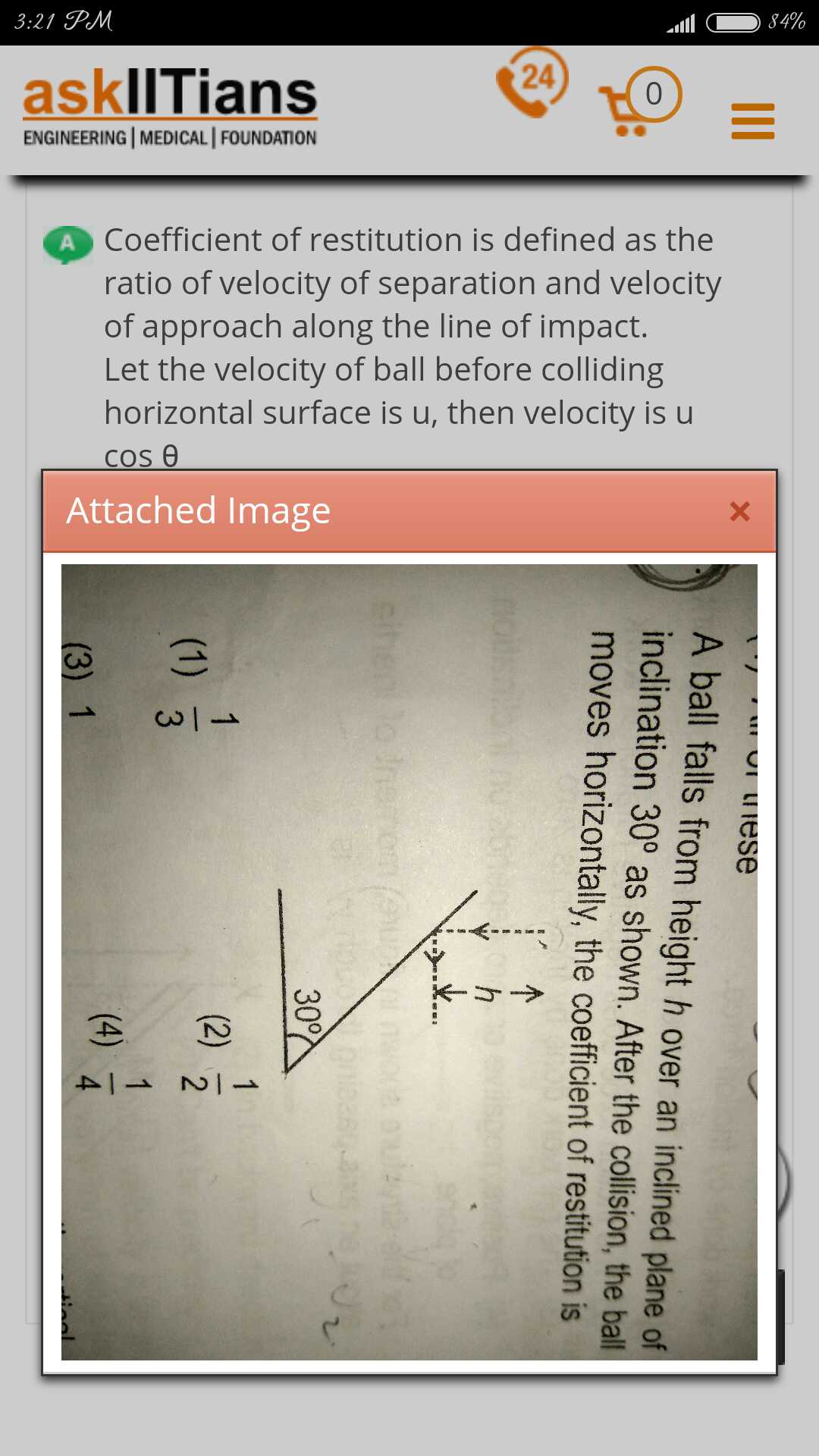
Let's break down your question step by step to clarify these concepts. It sounds like you're dealing with a physics problem related to collisions or impacts, which often involves angles and coefficients of restitution. We'll tackle the terms "line of impact," "vcostheta," and the equation "e = tan(2θ)" one by one.

Understanding the Line of Impact

The line of impact refers to the direction along which two objects collide. When two bodies collide, they exert forces on each other along this line. This is crucial because the behavior of the objects after the collision depends on how they interact along this line. For example, if two balls collide, the line of impact is the straight line that connects their centers at the moment of collision.

Visualizing the Line of Impact

Imagine two billiard balls on a pool table. When they collide, the line of impact is the line that runs through the centers of both balls at the moment of contact. The forces acting during the collision are directed along this line, which influences how the balls will bounce off each other.

Breaking Down vcostheta

Now, let's talk about "vcostheta." In physics, especially in problems involving angles, we often use trigonometric functions to resolve vectors into components. Here, "v" typically represents a velocity, and "theta" (θ) is the angle of incidence or impact.

• Velocity (v): This is the speed of an object in a specific direction.
• Cosine (cos): This function helps us find the adjacent side of a right triangle when we know the hypotenuse and the angle.

When we say "vcostheta," we are finding the component of the velocity that acts along the line of impact. This is important because only the part of the velocity that is directed along this line will affect the outcome of the collision.

Exploring the Equation e = tan(2θ)

The equation "e = tan(2θ)" relates to the coefficient of restitution (e), which measures how elastic a collision is. The coefficient of restitution is defined as the ratio of the relative speed after the collision to the relative speed before the collision along the line of impact.

To understand why e is expressed as tan(2θ), consider the following:

• Angle Doubling: The tangent function relates to the angles involved in the collision. When you double the angle (2θ), it reflects how the velocities change in relation to the angle of impact.
• Geometric Interpretation: In a right triangle formed by the velocities before and after the collision, the tangent of an angle is the ratio of the opposite side to the adjacent side. By using tan(2θ), we capture the relationship between the angles and the velocities involved in the collision.

Putting It All Together

In summary, the line of impact is crucial for understanding how two objects interact during a collision. The term "vcostheta" helps us find the effective velocity along this line, while the equation "e = tan(2θ)" connects the angle of impact to the elasticity of the collision. By grasping these concepts, you can better analyze and predict the outcomes of collisions in physics.

If you have any more questions or need further clarification on any part, feel free to ask! Understanding these principles will greatly enhance your grasp of dynamics and collisions.