In the given solution how do we find a_y and a_x from angular accn

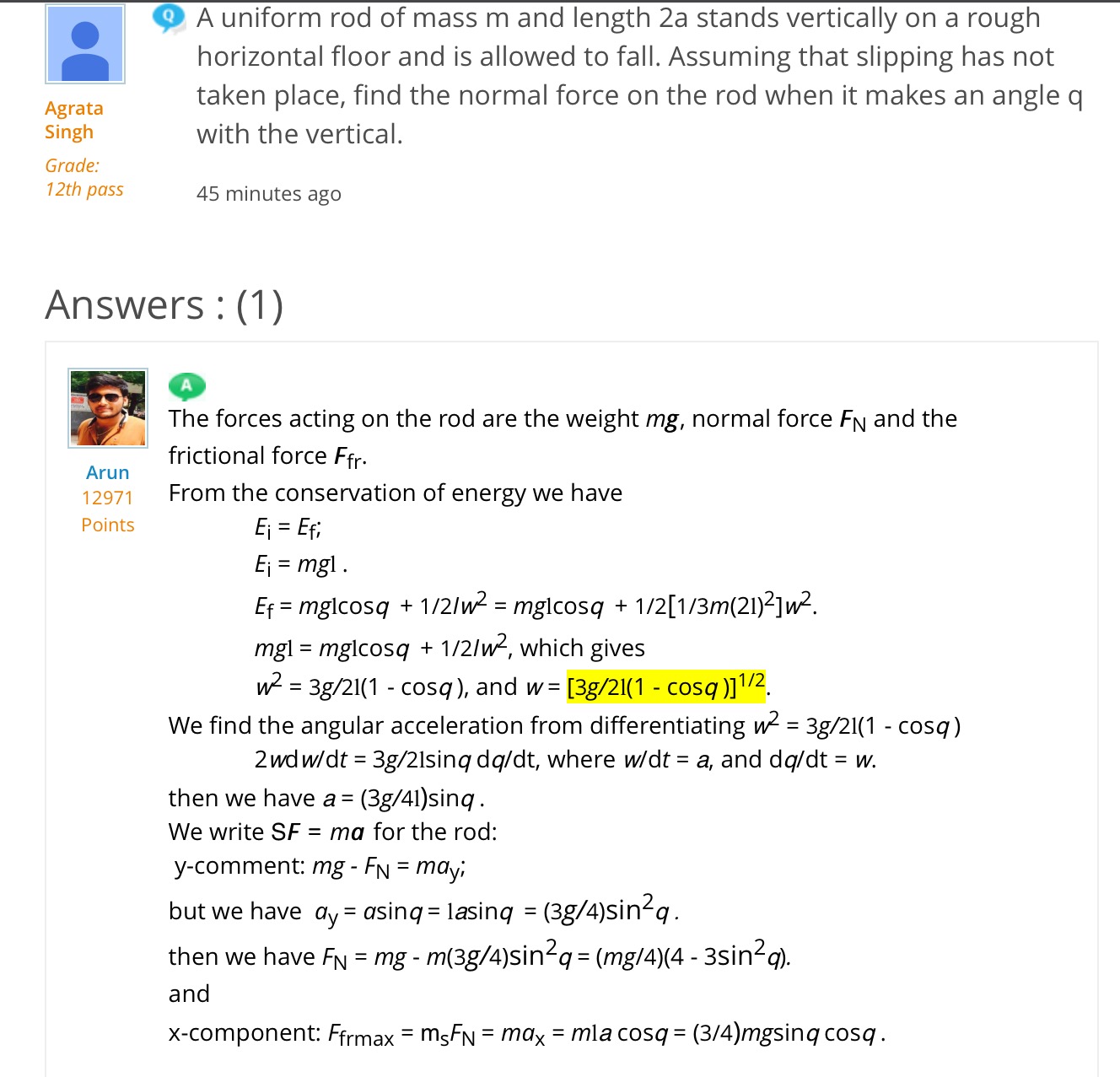
To find the values of \( y \) and \( x \) from angular acceleration, we first need to understand the relationship between angular acceleration and the angular displacement and velocity of an object. Angular acceleration, denoted as \( \alpha \), is defined as the rate of change of angular velocity over time. It can be expressed mathematically as:

Understanding Angular Acceleration

Angular acceleration can be calculated using the formula:

• \( \alpha = \frac{\Delta \omega}{\Delta t} \)

where \( \Delta \omega \) is the change in angular velocity and \( \Delta t \) is the change in time. This means that if you know how much the angular velocity changes over a specific time interval, you can determine the angular acceleration.

Finding Angular Displacement

To find the angular displacement \( \theta \) (which can be related to \( y \) in some contexts), we can use the following kinematic equation for rotational motion:

• \( \theta = \omega_0 t + \frac{1}{2} \alpha t^2 \)

In this equation, \( \omega_0 \) is the initial angular velocity, \( t \) is the time, and \( \alpha \) is the angular acceleration. By substituting known values into this equation, you can solve for \( \theta \), which may correspond to \( y \) in your specific problem.

Finding Linear Displacement

If you are looking for a linear displacement \( x \) related to the angular motion, you can use the relationship between linear and angular quantities. The linear displacement \( s \) is given by:

• \( s = r \theta \)

Here, \( r \) is the radius of the circular path. If you have calculated \( \theta \) from the previous step, you can find \( x \) by multiplying \( \theta \) by the radius \( r \). This relationship shows how angular motion translates into linear motion.

Example Calculation

Let’s say an object starts from rest (\( \omega_0 = 0 \)) and has an angular acceleration of \( 2 \, \text{rad/s}^2 \) for \( 3 \, \text{s} \). We can find \( \theta \) as follows:

• Using the equation for angular displacement: \( \theta = 0 \cdot 3 + \frac{1}{2} \cdot 2 \cdot (3^2) = 0 + 9 = 9 \, \text{rad} \)

If the radius \( r \) of the circular path is \( 1 \, \text{m} \), then the linear displacement \( x \) would be:

• \( x = r \theta = 1 \cdot 9 = 9 \, \text{m} \)

Summary of Steps

To summarize, finding \( y \) and \( x \) from angular acceleration involves:

• Calculating angular displacement \( \theta \) using the angular acceleration and time.
• Using the relationship between angular displacement and linear displacement to find \( x \).

By following these steps, you can effectively relate angular motion to linear motion and derive the necessary values from angular acceleration.