In response to my earlier question expert Vikas TU suggested a solution where the value of ‘x’ comes out to be 80 m. Kindly, refer to the new attached image and see the options. If x=80 m then none of the answers is correct. However, the answer in the key is D) root28 m/s. If x is 80m then u should be 10 m/s but there is no such option. I am a bit confused. Pls. help.

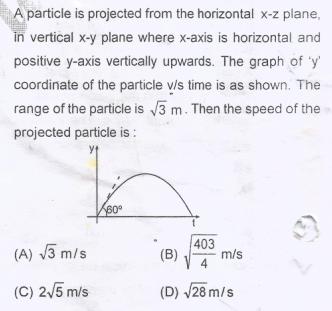
It sounds like you're grappling with a problem involving motion, possibly in a physics context. Let's break down the situation step by step to clarify the confusion surrounding the value of 'x' and the corresponding options provided.

Understanding the Problem

From what you've described, it seems that you have a scenario where 'x' represents a distance, and you're trying to determine the initial velocity 'u' based on that distance. If Vikas TU suggested that 'x' equals 80 m, we need to analyze how that relates to the other values and the answer key.

Analyzing the Given Values

First, let's consider the relationship between distance, initial velocity, and final velocity in motion. The equations of motion can help us here. One common equation is:

• s = ut + (1/2)at²

Where:

• s = distance (x)
• u = initial velocity
• a = acceleration
• t = time

If we assume there is no acceleration (a = 0), the equation simplifies to:

• s = ut

Calculating Initial Velocity

Given that 'x' is 80 m, if we assume a time 't' of 8 seconds (for example), we can rearrange the equation to find 'u':

• u = s/t = 80 m / 8 s = 10 m/s

However, you mentioned that there is no option for 10 m/s. This discrepancy suggests that either the time value is different or there is an acceleration involved that we haven't accounted for.

Exploring the Answer Key

The answer key indicates D) √28 m/s. Let's calculate what this value is:

• √28 ≈ 5.29 m/s

This value is significantly lower than the 10 m/s we calculated. If we consider the possibility of acceleration, we can use another equation of motion:

• v² = u² + 2as

Where 'v' is the final velocity. If we assume a final velocity of √28 m/s and solve for 'u' with 's' as 80 m, we can rearrange the equation:

• u² = v² - 2as

Substituting the values:

• u² = (√28)² - 2a(80)
• u² = 28 - 160a

From this, we can see that the initial velocity 'u' depends heavily on the acceleration 'a'. If 'a' is negative (deceleration), it could lead to a lower initial velocity. Without knowing the acceleration, we can't definitively conclude the initial velocity.

Final Thoughts

To resolve your confusion, I recommend checking the problem statement for any details regarding acceleration or time. If those values are provided, you can plug them into the equations to find a consistent answer. If not, it may be worth discussing with your instructor for clarification on the expected conditions of the problem.