Askiitians Tutor Team
Last Activity: 2 Months ago
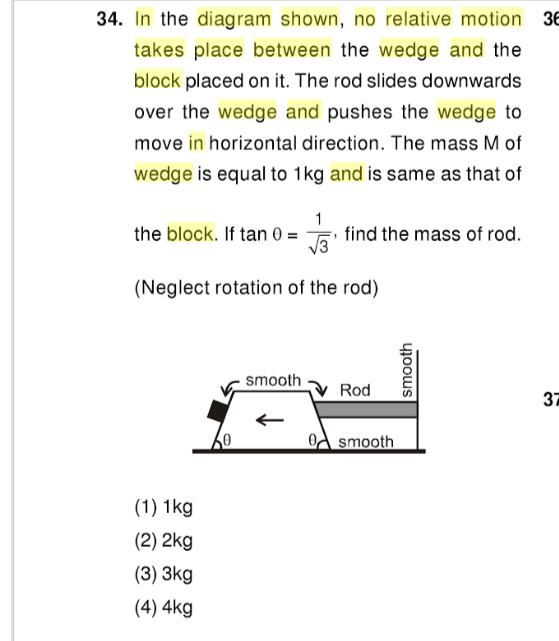
To solve this problem, we need to analyze the forces acting on the system without introducing pseudo forces. The scenario involves a wedge, a block resting on the wedge, and a rod that slides down the wedge, causing the wedge to move horizontally. Given that the mass of both the wedge and the block is 1 kg and that the angle of the wedge (theta) has a tangent value of 1/√3, we can derive the mass of the rod using principles of equilibrium and conservation of momentum.
Understanding the Forces at Play
First, let's clarify the setup. The wedge is inclined at an angle where tan(theta) = 1/√3, which means that theta = 30 degrees. The block on the wedge does not slide off due to the normal force acting perpendicular to the surface of the wedge. The rod, when it slides down, exerts a force on the wedge, causing it to move horizontally.
Analyzing the System
Since there is no relative motion between the wedge and the block, we can say that the horizontal component of the forces acting on the wedge must equal the horizontal component of the forces acting on the block. The forces can be broken down as follows:
- The weight of the block acting downwards: W_block = m_block * g = 1 kg * 9.81 m/s² = 9.81 N
- The normal force from the wedge on the block, which has a component acting horizontally.
Components of Forces
The normal force (N) acting on the block can be resolved into two components:
- Vertical component: N * cos(theta)
- Horizontal component: N * sin(theta)
Since the block is in equilibrium vertically, we can set the vertical component of the normal force equal to the weight of the block:
N * cos(theta) = W_block
Substituting the values, we have:
N * (√3/2) = 9.81 N
From this, we can solve for N:
N = 9.81 N / (√3/2) = 9.81 * (2/√3) ≈ 11.31 N
Finding the Horizontal Motion
The horizontal component of the normal force causes the wedge to move. Therefore, the horizontal force acting on the wedge is:
F_horizontal = N * sin(theta)
Substituting the value of N and sin(theta):
F_horizontal = 11.31 N * (1/2) ≈ 5.655 N
Applying Conservation of Momentum
Now, let’s consider the rod. As it slides down, it pushes the wedge horizontally. By conservation of momentum, the momentum of the rod must equal the momentum of the wedge plus the block. Since the wedge and block have equal mass, we can express this as:
m_rod * v_rod = (m_wedge + m_block) * v_wedge
Given that both the wedge and block have a mass of 1 kg, we can simplify this to:
m_rod * v_rod = 2 kg * v_wedge
Relating Velocities
Since the wedge moves horizontally due to the force exerted by the rod, we can relate the velocities. The velocity of the rod sliding down the wedge can be expressed in terms of the wedge's velocity:
v_rod = v_wedge / cos(theta)
Substituting this into our momentum equation gives:
m_rod * (v_wedge / cos(theta)) = 2 kg * v_wedge
Canceling out v_wedge (assuming it is not zero), we get:
m_rod / cos(theta) = 2 kg
Now, substituting cos(theta) = √3/2:
m_rod / (√3/2) = 2 kg
Solving for m_rod gives:
m_rod = 2 kg * (√3/2) = √3 kg ≈ 1.732 kg
Final Thoughts
Thus, the mass of the rod is approximately 1.732 kg. This approach effectively uses the principles of equilibrium and momentum without resorting to pseudo forces, providing a clear understanding of the dynamics involved in the system.