0

Guest

Courses New

Can we conserve energy in this question.. or is it because it's not bouncing so some energy wud hv gone as heat and sound.. so we cannot.. ? What's the significance of rod doesn't bounce And also if we cannot conserve energy.. how shall we do this?

Can we conserve energy in this question.. or is it because it's not bouncing so some energy wud hv gone as heat and sound.. so we cannot.. ? 
What's the significance of rod doesn't bounce 
And also if we cannot conserve energy.. how shall we do this?

Question Image
Grade:12

2 Answers

Ribhu Archon
28 Points
4 years ago
No energy is not conserved as there would be some impulse due to friction and collision with the ground may not be completely elastic.
 
But,
 
Since when it hits the ground the forces act between the ground and the rod, the combined system of the rod and ground can be considered as a system which has zero external force acting on it.
 
Hence ‘angular momentum of that system’ would be conserved.
 
Since ground is undergoing no change in its state of motion.(it is perpetually at rest...),we can just ‘say’ angular momentum of the rod is conserved
 
Significance of saying rough surface and does not bounce:
 
By saying the ground is rough they are restricting the rod’s slipping motion on ground. The rod will now get ‘hinged’ at a point (where it hits the ground) and rotate about that point. No bouncing also serves the same purpose. If the rod bounced, tracking its angular velocity becomes trickier (as the rod might start a translatory motion along with the rotatory motion).
 
Now onto the real solution:
 
Since in its downward motion there are absolutely no inhibitors. the rod performs a plain translatory motion untill it hits the ground. so untill that moment for all practical purposes we can consider the rod a point mass at the Center of Mass.
 
Since it falls through a distance h under a constant acceleration ‘g’ starting from rest Therefore:
 
final velocity:
 
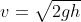
 v= \sqrt{2gh} (using equations of motion )
 
where v is the velocity of CM
 
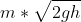
so just before the rod hits the ground momentum of rod is  m*\sqrt{2gh}
 
therefore angular momentum of the rod W.R.T. the point where it hits the ground= p x r
where p=momentum of rod and r=position vector of rod
 
Magnitude of angular momentum just before hitting the ground:
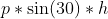
p*\sin(30)*h                                                          [positon vector to CM makes angle 30 degrees to
  velocity vector of rod and has magnitude ‘h’]
 
Also, after hitting the ground it gets hinged at the bottom most point and has an angular velocity \omega.
 
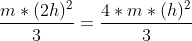
since its hinged at the bottom most point its Moment of Inertia is \frac{m*(2h)^2}{3}=\frac{4*m*(h)^2}{3}​
 
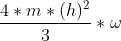
therfore angular momentum after collision \frac{4*m*(h)^2}{3}*\omega
 
But as we saw angular momentum of the rod is conserved.....
 
angular momentum initially=angular momentum finally
 
(m*\sqrt{2gh})*\sin(30)*h=\frac{4*m*(h)^2}{3}*\omega
 
 
we get,
 
\omega=\frac{3}{8}*\sqrt{\frac{2g}{h}}
 
 
from this we get  y=2 and x=8
 
therefore
 \frac{x}{y}=\frac{4}{1}
 
Vikas TU
14149 Points
3 years ago
An inelastic collisions occurs when two objects collide and do not bounce away from each other. Momentum is conserved, because the total momentum of both objects before and after the collision is the same. However, kinetic energy is not conserved. In an elastic collision, both momentum and kinetic energy are conserved.

Think You Can Provide A Better Answer ?

Other Related Questions on Mechanics

View all Questions »

ASK QUESTION

Get your questions answered by the expert for free

Answer and earn gift vouchers

Win Gift vouchers upto Rs 500/-

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Complete Self Study Package designed by Industry Leading Experts

Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child

Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Click Here Know More