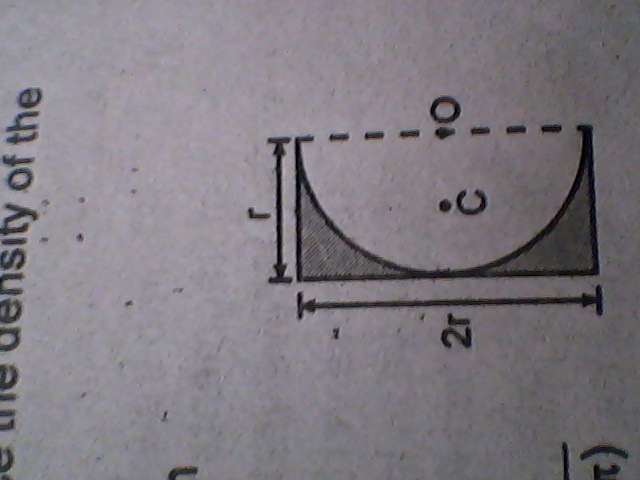A semicircular portion of radius r is cut from a uniform rectangular plate as shown in figure .the distance of centre of mass `c` of remaining plate from point `o`

To find the distance of the center of mass \( C \) of the remaining plate from point \( O \) after cutting out a semicircular portion, we can use the concept of the center of mass and the principle of superposition. This involves calculating the center of mass of the original rectangular plate and then adjusting for the mass removed by the semicircular cutout.

Understanding the Problem

Let's break this down step by step. Assume we have a rectangular plate with width \( W \) and height \( H \). A semicircular portion with radius \( r \) is cut from one of the corners of this rectangle. The goal is to determine the new center of mass of the remaining shape after this cut.

Step 1: Center of Mass of the Original Rectangle

The center of mass of a uniform rectangular plate is located at its geometric center. For a rectangle, this is at:

• X-coordinate: \( \frac{W}{2} \)
• Y-coordinate: \( \frac{H}{2} \)

Step 2: Center of Mass of the Semicircular Cutout

The center of mass of a semicircle lies along the vertical axis of symmetry, at a distance of \( \frac{4r}{3\pi} \) from the flat edge (the diameter). The coordinates of the center of mass of the semicircular cutout can be expressed as:

• X-coordinate: \( r \) (assuming the semicircle is cut from the left side)
• Y-coordinate: \( \frac{4r}{3\pi} \)

Step 3: Mass Calculations

Next, we need to calculate the mass of the rectangle and the semicircular cutout. Assuming uniform density \( \rho \):

• Mass of the rectangle \( M_r = \rho \cdot W \cdot H \)
• Mass of the semicircle \( M_s = \rho \cdot \frac{1}{2} \pi r^2 \cdot \frac{H}{2} = \frac{\rho \pi r^2 H}{4} \)

Step 4: Finding the New Center of Mass

Now, we can find the new center of mass \( C \) of the remaining shape using the formula for the center of mass of a system of particles:

• X-coordinate of \( C \):

  \( x_C = \frac{M_r \cdot \frac{W}{2} - M_s \cdot r}{M_r - M_s} \)

• Y-coordinate of \( C \):

  \( y_C = \frac{M_r \cdot \frac{H}{2} - M_s \cdot \frac{4r}{3\pi}}{M_r - M_s} \)

Step 5: Distance from Point O

Finally, the distance from point \( O \) (the bottom left corner of the rectangle) to the center of mass \( C \) can be calculated using the Pythagorean theorem:

\( d = \sqrt{x_C^2 + y_C^2} \)

By substituting the expressions for \( x_C \) and \( y_C \) into this equation, you can find the exact distance of the center of mass of the remaining plate from point \( O \).

This approach combines geometry and physics principles to arrive at a solution, illustrating how the removal of mass affects the overall center of mass of a composite shape. If you have any specific values for \( W \), \( H \), or \( r \), we can plug those in to get a numerical answer!