Other Related Questions on mechanics

Three identical balls are placed on a frictionless
horizontal surface touching each other. They stick to
each other because of adhesive. Another ball of same
radius and mass m is placed over the void created by
the three balls. Find the forces applied by the balls
kept on the floor to each other if the system remains
in equilibrium.
Three identical balls are placed on a frictionless
horizontal surface touching each other. They stick to
each other because of adhesive. Another ball of same
radius and mass m is placed over the void created by
the three balls. Find the forces applied by the balls
kept on the floor to each other if the system remains
in equilibrium.
mechanics
Last Activity: 4 Months ago

A car loaded with water having total mass 1000 kg moves on a straight horizontal Road starting from rest under the action of a force of 100 Newton. The water spills throw a small hole in the bottom at a rate of 0.1 KG per second the velocity of cart after 300 seconds is nearly.
11
21
31
41
A car loaded with water having total mass 1000 kg moves on a straight horizontal Road starting from rest under the action of a force of 100 Newton. The water spills throw a small hole in the bottom at a rate of 0.1 KG per second the velocity of cart after 300 seconds is nearly.
11
21
31
41
mechanics
Last Activity: 4 Months ago

A metal strip clamped at one end vibrates with a frequency of 20 Hz and amplitude of 5 mmat the free end, where a small mass of 2 g is positioned. determine(i) The velocity of the end when passing through the zero position(ii) The acceleration at maximum displacement(iii) The maximum kinetic energy of the mass
mechanics
Last Activity: 3 Years ago

An object of mass m = 0.25 kg oscillates in a fluid at the end of a vertical spring of springconstant kH = 85 N/m, see Fig.1. The effect of the fluid resistance is governed by thedamping constant b = 0.07kg/s.(i) Find the period of the damped oscillation.(ii) By what percentage does the amplitude of the oscillation decrease in each cycle?
mechanics
Last Activity: 3 Years ago

If a=x² find the displacement at t =3sec if body velocity at t= 0 sec is 0
mechanics
Last Activity: 3 Years ago






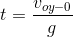 …… (1)
…… (1)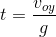



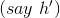 and was thrown upward with initial v0yspeed on Planet. Therefore the downward acceleration experienced by the stone is equal to the acceleration due to gravity on Planet i.e.2g .
and was thrown upward with initial v0yspeed on Planet. Therefore the downward acceleration experienced by the stone is equal to the acceleration due to gravity on Planet i.e.2g .

 …… (2)
…… (2)
 , the equation above changes to
, the equation above changes to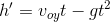

 , we have
, we have






