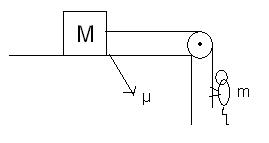
AMonkey of mass m climbs up to a rope hung over a fixed pulleywithacceleration g/4. The opposite end of the rope is tied to a blockofmass M lying on a rough horizontal plane. The coefficient offrictionbetween the block and horizontal plane is μ. Find the tension in the rope.

As monkey is accelerating upwards by g/4 it must be applying its mass times its acceleration force downwards.

THUS

Force ON ROPE

by monkey :- m*(g/4) downwards + its mass times acceleration due to gravity     i.e m*g

F_net=m(g+g/4)= 5mg/4 which equals the tension.

till F_net≤µMg

I tried this question and was able to solve!

Acceleration of Monkey/Rope = g/4

Let the acceleration of ''M'' = a

So, the acceleration of the rope = a

(a)_monkey = (a)_monkey/rope + (a)_rope

               = (a-g/4)

For mass M, T - μmg = Ma                        ...(1)

For Monkey, mg - T = m(a - g/4)              ...(2)

From equation (1) and (2),

mg - μMg = a(M + m) - mg/4

Then,

a = (5m/4 - μM)g / (M + m) = (5m - 4μM)g / 4(M + m)

Therefore, T = [M(5m - 4μM)g / 4(M + m)] - μMg