Ask a Doubt
Get your questions answered by the expert for free
Enter text here...
Other Related Questions on Mechanics

A metal strip clamped at one end vibrates with a frequency of 20 Hz and amplitude of 5 mmat the free end, where a small mass of 2 g is positioned. determine(i) The velocity of the end when passing through the zero position(ii) The acceleration at maximum displacement(iii) The maximum kinetic energy of the mass
Mechanics
2 Answer Available
Last Activity: 2 Year ago(s)

An object of mass m = 0.25 kg oscillates in a fluid at the end of a vertical spring of springconstant kH = 85 N/m, see Fig.1. The effect of the fluid resistance is governed by thedamping constant b = 0.07kg/s.(i) Find the period of the damped oscillation.(ii) By what percentage does the amplitude of the oscillation decrease in each cycle?
Mechanics
1 Answer Available
Last Activity: 2 Year ago(s)

If a=x² find the displacement at t =3sec if body velocity at t= 0 sec is 0
Mechanics
1 Answer Available
Last Activity: 2 Year ago(s)

A particle is traveling in a circle of radius R =2.5m and with an angular velocity of 10 rad/s. What is the centripetal acceleration of the particle? The particle begins to slow down with an angular acceleration of -1 rad/s2. After 5 seconds, what is the centripetal acceleration and the tangential acceleration fo the particle?
Mechanics
1 Answer Available
Last Activity: 2 Year ago(s)

If the acceleration of block A is 5 m/s^2Find the acceleration of block B
Mechanics
1 Answer Available
Last Activity: 2 Year ago(s)





 and
and 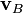 respectively in terms of a given coordinate system, then the relative velocity of A with respect to B (also called the velocity of A relative to B,
respectively in terms of a given coordinate system, then the relative velocity of A with respect to B (also called the velocity of A relative to B, 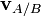 , or
, or  ) is
) is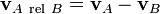 .
. .
.



