To determine the number of revolutions the fan makes after being hit by the bullet, we need to analyze the forces acting on the fan and how they relate to its motion. The key here is to understand the concepts of torque, angular momentum, and the relationship between force and rotational motion.

Understanding the Forces Involved

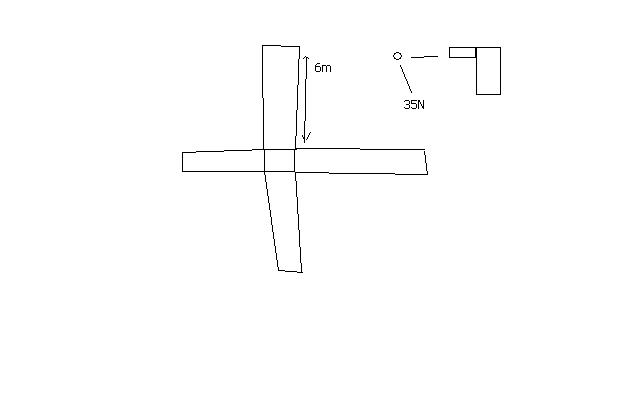
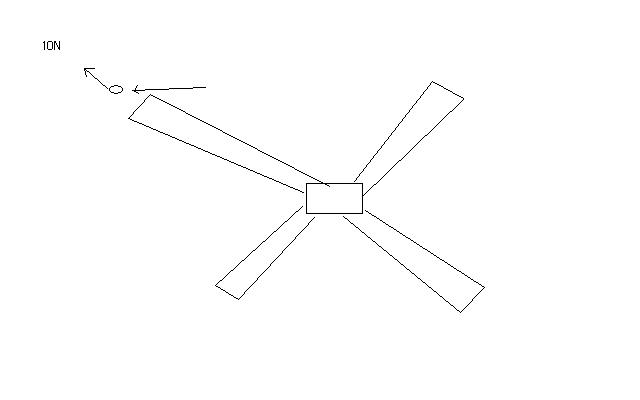
When the bullet strikes the fan, it applies a force of 35 N on one side and exits with a force of 10 N on the opposite side. The difference in these forces will create a net torque on the fan, which will cause it to rotate.

Calculating the Net Force

The net force acting on the fan can be calculated as follows:

• Force in: 35 N
• Force out: 10 N
• Net Force = Force in - Force out = 35 N - 10 N = 25 N

Torque Calculation

Torque (\( \tau \)) is calculated using the formula:

Torque = Force × Distance

In this case, the distance is the length of the fan blade, which is 6 m. Therefore, the torque generated by the net force is:

Torque = 25 N × 6 m = 150 N·m

Relating Torque to Angular Motion

Next, we need to relate this torque to the angular motion of the fan. The moment of inertia (I) of a single blade can be approximated for a thin rod rotating about one end using the formula:

I = (1/3) × m × L²

Where:

• m = mass of the blade
• L = length of the blade

Given that the weight of one blade is 0.5 N, we can find the mass (m) using the relation \( Weight = mass × g \), where \( g \) is approximately 9.81 m/s²:

m = Weight / g = 0.5 N / 9.81 m/s² ≈ 0.051 kg

Now, substituting the values into the moment of inertia formula:

I = (1/3) × 0.051 kg × (6 m)² = (1/3) × 0.051 kg × 36 m² ≈ 0.612 kg·m²

Finding Angular Acceleration

Using Newton's second law for rotation, we can find the angular acceleration (\( \alpha \)):

Torque = I × α

Rearranging gives:

α = Torque / I = 150 N·m / 0.612 kg·m² ≈ 245.4 rad/s²

Calculating the Number of Revolutions

To find the number of revolutions, we need to know how long the fan rotates under this angular acceleration. Assuming the bullet impact causes an instantaneous change in motion, we can consider the fan to start from rest. The angular displacement (\( \theta \)) in radians can be calculated using the formula:

θ = (1/2) × α × t²

However, we need to define a time duration (t) for which the fan continues to rotate. If we assume the fan continues to rotate for a short time after the impact, we can estimate the number of revolutions based on a hypothetical time. Let's say the fan rotates for 1 second:

θ = (1/2) × 245.4 rad/s² × (1 s)² = 122.7 rad

To convert radians to revolutions, we use the conversion factor \( 1 \text{ revolution} = 2π \text{ radians} \):

Number of revolutions = θ / (2π) = 122.7 rad / (2π) ≈ 19.5 revolutions

Final Thoughts

In this scenario, if the fan rotates for approximately 1 second after being struck, it would complete about 19.5 revolutions. The exact number of revolutions could vary based on the actual time the fan continues to spin after the impact, but this gives you a solid estimate based on the forces and torques involved.