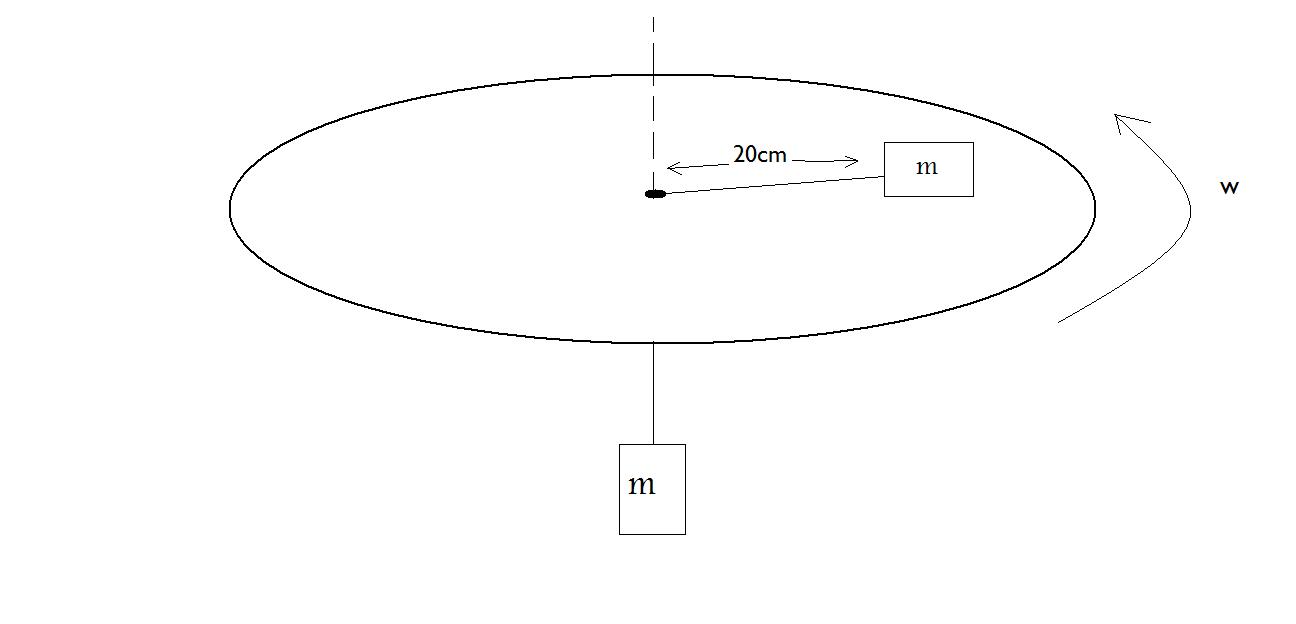
A table is rotating about its axis through its centre. Two equal masses are fixed at both the ends of a thread passing through a hole in the centre. The body on the table is 20cm away from the centre. What will be the rpm of the table when the body below the table will hang motionlessly??

am not able to visulize the problem.

van u pls post a picture?

Hi Subhajit

Let the mass of both the bodies be m

The body which is on the table is performing a circular motion of radius 20cm.

The tension in the string is equal to the centripetal force on the body placed on the table.

                                         T=m[omega)^2]R                   ...............(!)

Here R=20cm and omega is the angular velocity of the table or angular velocity of the body

The body which is hanging below the table is stationary.

Therefore, tension in the string is equal to the weight of the hanging body

                                    T=mg               ........................(2)

From equation(1) and Equation(2)

                  mg=m[omega)^2]R

       =>    g=[omega)^2]R =>omega= 7 radian/second =420 radian/minute

Hence , the body is performing 420 revolutions per minute.

As the question says that table is rotating,therefore angular velocity of the body is equal to the angular velcoty of the table.

Hence,table is making 420 revolutions per minute.