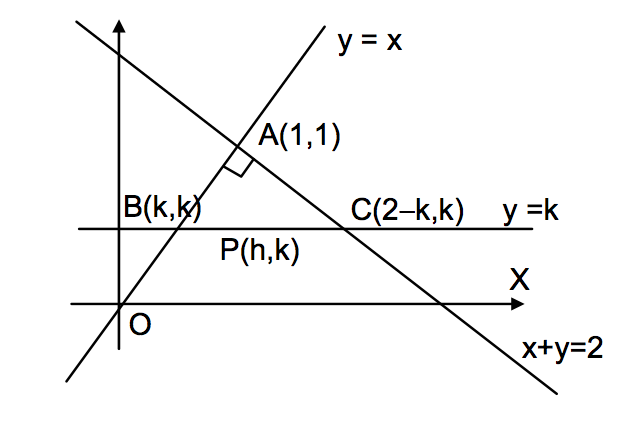
The area of the triangle formed by the intersection of a line parallel to x-axis and passing through P (h, k) with the lines y = x and x + y = 2 is 4h^2. Find the locus of the point P.
The area of the triangle formed by the intersection of a line parallel to x-axis and passing through P (h, k) with the lines y = x and x + y = 2 is 4h^2. Find the locus of the point P.
Matt Farrel , 10 Years ago
Grade 10
