0

Guest

Courses New

A positive integer n is randomly guesses. Let the probability that (x n+1 - x n +1) is divisible by (x 2 - x +1) is P . Find P

A positive integer n is randomly guesses. Let the probability that (xn+1- xn +1) is divisible by (x2 - x +1) is P . Find P

Grade:12

2 Answers

Ribhu Archon
28 Points
4 years ago
This question is based on complex numbers so.....
 
Let’s assume an equation  x^3=-1
 
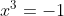
therefore,
 
x^3+1=0
So all roots of the above cubic equation except 1 are roots of  x^2-x+1
 
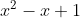
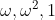
Now we know roots of are  \omega,\omega^2,1
  \therefore(-x)^3=-1
So  (-\omega)^3=-1    ,    (-\omega^2)^3=-1   ,    (-1)^3=-1
 
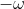
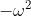
Clearly roots of the first equation are  -\omega   ,  -\omega^2   ,-1
 
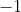
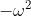
putting  \omegain and simplifying we get, [we can put -\omega^2, but i’ll come to that later][step a]
 
(\omega)^{n+1}*(-1)^{n+1}+(-1)*(\omega)^{n}*(-1)^{n}+1=0
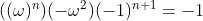
((\omega)^{n})(-\omega^2)(-1)^{n+1}=-1         
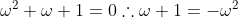
                                                      [\omega^2+\omega+1=0\therefore\omega+1=-\omega^2 ]
 
\therefore\omega^{n+2}=(-1)^{n+3}
 
Since a power of  \omega  is giving a real number, that power must be a multiple of 3.  Hence n+2 is divisible by 3
 
also the only real result of a power of omega is 1. hence the power of -1 is even. Hence n+3 is divisible by 2
 
thus n is odd (from n+3 is divisible by 2) and n leaves a remainder 1 when divide by 3 (from n+2 is divisible by 3)
 
let’s now list out the possibilties,..
 
{\color{Red} 1}, 2 ,3 ,4 ,5 ,6 ,{\color{Red} 7} ,8 ,9,10,11,12,{\color{Red} 13},14,15,16,17,18,{\color{Red} 19}....
Notice how every 6 possibilities there is one such number
 
let the sample space thus be 6*q [q being any integer], there would be q favourable outcomes.
as the sample space is infinite (no restriction given) we can assume that even though the sample space is infinite this ‘infinity’ is divisible by 6 [any other case would be mathematically insignificant]
 
thus probability is 
P=\lim_{q\to\infty}\frac{q}{6*q}=\frac{1}{6}
 
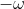
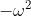
the same will actually happen if in [step a] instead of -\omega we put -\omega^2
(-\omega^2)^{n+1}-(-w^2)^{n}+1=0
 
((\omega^2)^{n})(\omega^2+1)(-1)^{n+1}=-1
((\omega^2)^{n})(-\omega)(-1)^{n+1}=-1 [\omega^2+\omega+1=0\therefore\omega^2+1=-\omega]
((\omega)^{2n+1})(-1)^{n+2}=-1
 
\therefore\omega^{2n+1}=(-1)^{n+3}
 
Since a power of  \omega  is giving a real number, that power must be a multiple of 3.  Hence 2n+1 is divisible by 3
 
also the only real result of a power of omega is 1. hence the power of -1 is even. Hence n+3 is divisible by 2
 
thus n is odd (from n+3 is divisible by 2) and 2n leaves a remainder 2 when divided by 3 (from 2n+1 is divisible by 3)
 
listing out the possibilities again....
 
{\color{Blue} 1}, 2 ,3 ,4 ,5 ,6 ,{\color{Blue} 7} ,8 ,9,10,11,12,{\color{Blue} 13},14,15,16,17,18,{\color{Blue} 19}....
the same result the same equation and thus the same value:
 
P=\lim_{q\to\infty}\frac{q}{6*q}=\frac{1}{6}
hence,
 
P=\frac{1}{6}
Vikas TU
14149 Points
4 years ago
Dear student 
Please ask question related to syllabus .
This kind of questions will not be asked.
Good Luck 
Cheers 

Think You Can Provide A Better Answer ?

Other Related Questions on Magical Mathematics[Interesting Approach]

View all Questions »

ASK QUESTION

Get your questions answered by the expert for free

Answer and earn gift vouchers

Win Gift vouchers upto Rs 500/-

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Complete Self Study Package designed by Industry Leading Experts

Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child

Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Click Here Know More