1800-150-456-789
FlagBACK
Flag Integral Calculus> if integral 1+tan(x-a)tan(x+a)dx=B ln(cos...
question mark

if integral 1+tan(x-a)tan(x+a)dx=B ln(cos(x+a)/cos(x-a))+c then find B
  1. cot2a
  2. tan2a
  3. -cot2a
  4. -tan2a

chandrika , 6 Years ago
Grade 12th pass
anser 1 Answers
Samyak Jain

Last Activity: 6 Years ago

1 + tan(x – a) tan(x + a)   =   1 + {sin(x – a)/cos(x – a)} {sin(x + a)/cos(x + a)}  
                                                       ...Using tanA = sinA / cosA
                   = [cos(x + a)cos(x – a) + sin(x + a)sin(x – a)] / [cos(x + a)cos(x – a)]           
                   = cos{(x + a) – (x – a)} / cos(x + a)cos(x – a)  =  cos(2a) / cos(x + a)cos(x – a)
    ...Using cosAcosB + sinAsinB = cos(A – B)
                   = sin(2a)/sin(2a) x cos(2a) / cos(x + a)cos(x – a)
                   = cot(2a) . sin2a / cos(x + a)cos(x – a)  =  cot(2a) sin{(x+a) – (x–a)} / cos(x + a)cos(x – a)
                   = cot(2a) . [sin(x+a)cos(x–a) – cos(x+a)sin(x–a)] / cos(x + a)cos(x – a)
   … Using sin(A – B) = sinAcosB – cosAsinB
                   = cot(2a) [tan(x+a) – tan(x–a)]
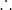
\therefore ∫ [1 + tan(x – a) tan(x + a)]dx  =  ∫cot(2a) [tan(x+a) – tan(x–a)]dx
              =  cot(2a) [∫ tan(x+a) dx – ∫ tan(x–a) dx]    =   cot(2a)[ln(sec(x+a) – ln(sec(x–a))] + c
              =  cot(2a) ln(sec(x + a) / sec(x – a)) + c    =  cot(2a) ln(cos(x – a) / cos(x + a)) + c
              =  cot(2a) [– ln(cos(x + a) / cos(x – a))] + c
              =  – cot(2a) ln(cos(x + a) / cos(x – a)) + c
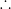\therefore B = – cot(2a)

star
LIVE ONLINE CLASSES

Prepraring for the competition made easy just by live online class.

tv

Full Live Access

material

Study Material

removal

Live Doubts Solving

assignment

Daily Class Assignments


Other Related Questions on integral calculus

question mark
The area of a square field is 640000cm2.what is its area in hectares
integral calculus
1 Answer Available

Last Activity: 2 Years ago

question mark
Please solve this integration. I am facing difficulty in it
 How to solve this. Please solve anyone. Humble request
integral calculus
0 Answer Available

Last Activity: 3 Years ago

question mark
Using laplace transform, solve d2y/dt2 + dy/dt = t2 +2t given that y=4 and y’=-2 and t=0
integral calculus
0 Answer Available

Last Activity: 3 Years ago

question mark
how to solve this?
this is interger type question .
integral calculus
0 Answer Available

Last Activity: 3 Years ago