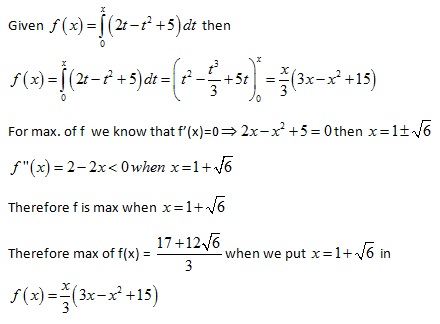find the maximum value of f(x) =integration of 0 to x (2t-t²+5)dt
kenadi kumar , 11 Years ago
Grade 12
Integral Calculus> find the maximum value of f(x) =integrati...
3 Answerslokesh palingi
Last Activity: 11 Years ago
on integrating using lebnitz theorem for differantiation under integral sign df(x)/dx=2x-x2+5 for maxima and minima df(x)/dx=0 =>2x-x2+5=0 => x= 1+sqrt(6),1-sqrt(6) d2f(x)/dx2=2-2x ,d2f(x)/dx2=sqrt(6) for x= 1-sqrt(6) and ,d2f(x)/dx2=-sqrt(6) for x= 1+sqrt(6) thus f(x) is maximum for x= 1+sqrt(6) as,d2f(x)/dx2=-sqrt(6)<0 thus maximum value of f(x)=integral 0 to1+sqrt(6)(2t-t²+5)dt = (t2-t3/3+5t)01+sqrt(6) =17/3 + 4sqrt(6)
MuraliKrishna Medavaram
Last Activity: 11 Years ago
Thanks and Regards,
M.MURALIKRISHNA
askIITians faculty
MuraliKrishna Medavaram
Last Activity: 11 Years ago
a
Provide a better Answer & Earn Cool Goodies
Enter text here...
LIVE ONLINE CLASSES
Prepraring for the competition made easy just by live online class.
Full Live Access
Study Material
Live Doubts Solving
Daily Class Assignments
Ask a Doubt
Get your questions answered by the expert for free
Enter text here...
Other Related Questions on integral calculus
The area of a square field is 640000cm2.what is its area in hectares
integral calculus
1 Answer Available
Last Activity: 2 Years ago
Please solve this integration. I am facing difficulty in it How to solve this. Please solve anyone. Humble request
integral calculus
0 Answer Available
Last Activity: 2 Years ago
Using laplace transform, solve d2y/dt2 + dy/dt = t2 +2t given that y=4 and y’=-2 and t=0
integral calculus
0 Answer Available
Last Activity: 2 Years ago
how to solve this?this is interger type question .
integral calculus
0 Answer Available
Last Activity: 3 Years ago
Find the integral of x/(1+cos^2x) from -pi/2 to pi/2
integral calculus
0 Answer Available
Last Activity: 3 Years ago