0

Guest

Courses New

Please provide the Attached questions.This is from NLM and friction

Please provide the Attached questions.This is from NLM and friction

Question Image
Grade:10

1 Answers

Samyak Jain
333 Points
5 years ago
mA = 6 kg, mB = 3 kg, mC = 6 kg, mD = 1 kg,
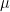\mu1 = 0.7 = friction coefficient between A and B, 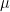\mu2 = 0.2 = friction coefficient between surface and B.
Let us assume that the system has a common acceleration ‘a’ i.e. C is moving downwards, A and B are moving together to the left and D is moving upwards with same acceleration a.
 
Let T1 and T2 be the tensions in the strings connecting blocks A and C and blocks B and D, N1 be the normal reaction between A and B, N2 be the normal reaction between surface and B, f1 be the force of friction between A and B, f2 be the frictional force between the surface and B.
 
FBDs (free body diagrams) of the blocks are shown below.
                    T1                                     N1                                              N2
                    \uparrow                                      \uparrow                                                \uparrow
Block C :   |  6 kg  |   ,  Block A :  T1 \leftarrow |  6 kg  | \rightarrow f1  ,  Block B : f1 \leftarrow | 3 kg | \rightarrow T2 + f2
                     \downarrow                                       \downarrow                                            \downarrow      \downarrow
             mc g = 60 N                      mA g = 60 N                                     N1   mB g = 30 N
            
                  T2
                   \uparrow
Block D :  | 1 kg |
                   \downarrow
              mD g = 10 N
There isn’t vertical motion of A and B i.e. net force acting on them in vertical direction is zero.
N1 = mA g = 60 N  and  N2 = N1 + mB g  \Rightarrow N2 = (60 + 30) N = 90 N.
Limiting static friction or kinetic friction between A and B is
f1max = 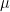\mu1 N1 = (0.7)(60) = 42 N.
Similarly, maximum static friction or kinetic friction between B and the surface is
f2max = (0.2)(90) = 18 N.
Since we have assumed that A and B are moving together, B is sliding on the surface and the associated friction is kinetic. So, f2 = 18 N.
Applying Fnet = m.a for each mass, we get
For C,  60 – T1 = 6 a                             ...(1)
For A,  T1 – f1  = 6 a                             ...(2)
For B,  f1 – T2 – f2 = 3 a  \Rightarrow  f1 – T2 – 18 = 3 a                      ...(3)
For D,  T2 – 10 = 1 a                             ...(4)
Add (1), (2), (3) & (4) \Rightarrow 60 – 18 – 10 = (6+6+3+1) a  \Rightarrow 32 = 16a or a = 2 m/s2
Put the value of a in (1), (2), (3), (4) to get
T1 = 48 N , T2 = 12 N , f1 = 36 N    f1max.
\because f1 1max , our assumption is correct.
Thus, options ‘A’ and ‘D’ are correct.

Think You Can Provide A Better Answer ?

Other Related Questions on IIT JEE Entrance Exam

View all Questions »

ASK QUESTION

Get your questions answered by the expert for free

Answer and earn gift vouchers

Win Gift vouchers upto Rs 500/-

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Complete Self Study Package designed by Industry Leading Experts

Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child

Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Click Here Know More