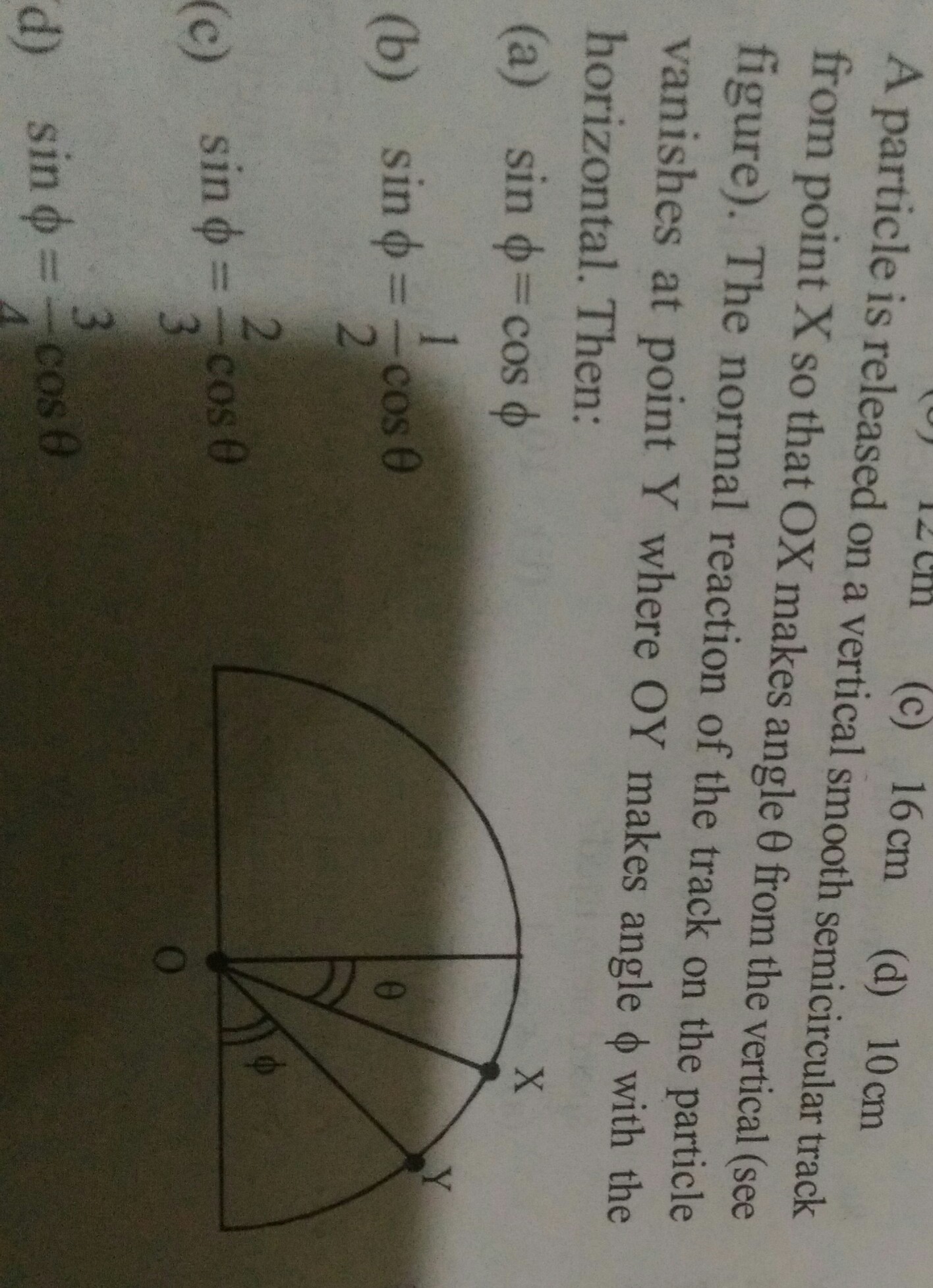
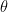Let mass of particle be m, radius of semicircular track be R and acceleration due to gravity is g.
Weight of particle is mg.
At point X, let normal reaction of track be N. Resolve the weight (mg) vector along the radius (which is mgcos
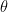
) and tangent to the track (which is mgsin
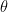
). Since initial velocity is zero, net centripetal force N – mgcos
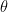
= 0.
The particle will descend the track due to mgsin
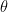
component.
We can apply energy conservation here because surface of semicircle is smooth, work done by normal reaction is zero and weight of the particle is conservative force i.e. there is no non-conservative force.
i.e. Loss in potential energy = Gain in kinetic energy ….(1)
Clearly, vertical displacement of particle from X to Y is h = Rcos
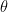
– Rsin
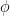
=
R(cos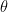 – sin
– sin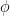 )
).
loss in potential energy =
mgh = mgR(cos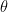 – sin
– sin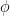 )
) ….(2)
Let speed of the paricle at point Y be v. Also, its initial speed is zero.
Then gain in kinetic energy = (1/2)mv2 – (1/2)m02 = (1/2)mv2 ….(3)
From (1),(2) & (3),
mgR(cos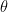 – sin
– sin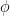 ) = (1/2)mv2
) = (1/2)mv2 ….(4)
Now, consider point Y. Resolve mg radially and tangentially.
Radial component of mg = mg sin
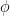
and tangential component of mg = mg cos
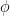
.
It is given at point Y, normal reaction vanishes i.e. N = 0.
Net centripetal force is mg sin
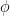
= mv
2 / R
mv
2 = mgR sin
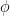
.
Substitute the value of mv2 in (4). We get
mgR(cos
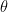
– sin
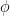
) = (1/2)mgR sin
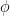
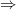
2cos
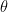
– 2sin
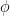
= sin
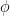
2cos
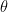
= 3sin
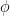
or sin
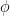
= (2/3) cos