IIT JEE Entrance Exam> Please explain how the solve the image pr...

Please explain how the solve the image problem please explain fully clearly......!..............

sudhanva gv , 5 Years ago

Grade

1 Answers

Samyak Jain

Last Activity: 5 Years ago

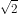
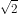
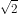
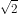
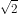
1 + i = $\sqrt{2}$ (1/ $\sqrt{2}$ + i.1/ $\sqrt{2}$ ) = $\sqrt{2}$ (cos $\pi$ /4 + i sin $\pi$ /4) = $\sqrt{2}$ .e^(i. $\pi$ /4) [Euler’s form of complex number]

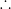
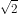
$\therefore$ z = log₂ (1 + i) = log₂ ( $\sqrt{2}$ .e^(i. $\pi$ /4))

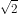
and z(bar) = log₂ ( $\sqrt{2}$ .e^(– i. $\pi$ /4))

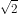
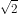
z + z(bar) = log₂ ( $\sqrt{2}$ .e^(i. $\pi$ /4)) + log₂ ( $\sqrt{2}$ .e^(– i. $\pi$ /4))

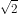
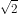
= log₂ ( $\sqrt{2}$ .e^(i. $\pi$ /4). $\sqrt{2}$ .e^(– i. $\pi$ /4)) = log₂ (2)

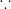
= 1 [ $\because$ log_c a + log_cb = log_c ab and log_aa = 1]

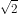
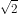
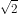
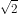
z – z(bar) = log₂ ( $\sqrt{2}$ .e^(– i. $\pi$ /4)) – log₂ ( $\sqrt{2}$ .e^(i. $\pi$ /4)) = log₂ ( $\sqrt{2}$ .e^(i. $\pi$ /4) / ( $\sqrt{2}$ .e^(– i. $\pi$ /4))
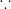
= log₂ (e^(i $\pi$ /4 + i $\pi$ /4)) = log₂ (e^(i $\pi$ /2)) [ $\because$ log_c a – log_cb = log_c a/b]

= log_e (e^(i $\pi$ /2)) / log_e 2 using change of base law of logarithm.

= (i $\pi$ /2) / ln2

= i $\pi$ /2.ln2 = i. $\pi$ /ln2² = i. $\pi$ /ln4

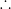
$\therefore$ z + z(bar) + i(z – z(bar)) = 1 + i(i. $\pi$ /ln4) = 1 + i². $\pi$ /ln4 = 1 – $\pi$ /ln4 [i² = – 1]

= (ln4 – $\pi$ ) / ln4.