help@askiitians.com

1800-150-456-789

IIT JEE Entrance Exam> PleaPl help me with the question given in...

question mark

PleaPl help me with the question given in the image attachment.

Anshu Mishra , 5 Years ago

Grade 12th pass

2 Answers

Arun

Last Activity: 5 Years ago

Lim x->a (cos x - cos a / cot x - cot a)
= Lim x->a (cos x - cos a) / [(cos x sin a - cos a sin x)/(sin x sin a)]
= Lim x->a (-2sin((x-a)/2)sin((x+a)/2)) / [(sin(a-x))/(sin x sin a)]
= sin^3 a
---------
Ideas: cos x - cos a = cos[(x+a)/2 + (x-a)/2] - cos[(x+a)/2 - (x-a)/2] = -2sin((x-a)/2)sin((x+a)/2)

Samyak Jain

Last Activity: 5 Years ago

lim (cosx – cosa) / (cotx – cota) It is of 0 by 0 form. Simplifying it we can calculate the limit.

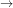
x $\rightarrow$ a

We know cosx – cosa = 2 sin(x+a)/2 sin(a – x)/2 and

cotx – cota = cosx/sinx – cosa/sina = (sina cosx – cosa sinx) / sinx sina = sin(a – x) / sinx sina

$\therefore$ lim (cosx – cosa) / (cotx – cota) = lim [2 sin(x+a)/2 sin(a – x)/2] / [sin(a – x) / sinx sina]

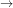
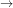
x $\rightarrow$ a x $\rightarrow$ a

= lim [2 sin(x+a)/2 sin(a – x)/2 . sinx sina ] / [2 sin (a – x)/2 cos(a – x)/2 ]

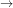
x $\rightarrow$ a

= lim sin(x+a)/2 . sinx sina / cos(a – x)/2 = sina lim sin(x+a)/2 . sinx / lim cos(a – x)/2

x $\rightarrow$ a x $\rightarrow$ a x $\rightarrow$ a

= sina sin(a+a)/2 . sina / cos(a – a)/2 = sina sina .sina / cos0

= sin³a

Provide a better Answer & Earn Cool Goodies

Enter text here...

LIVE ONLINE CLASSES

Prepraring for the competition made easy just by live online class.

Full Live Access

Study Material

Live Doubts Solving

Daily Class Assignments

Ask a Doubt

Get your questions answered by the expert for free

Enter text here...

question mark

My rank is 29k, General, should I opt for any state college cse branch or some Nits in which in which I am getting ECE , chemical, mechanics etc....

IIT JEE Entrance Exam

0 Answer Available

Last Activity: 2 Year ago(s)

question mark

How is Ranquer Eduzone,comparing, Akash,Fitjee,Resonance,Naryana

IIT JEE Entrance Exam

0 Answer Available

Last Activity: 2 Year ago(s)

question mark

Can class 9th students study syllabus classof 11th

IIT JEE Entrance Exam

3 Answer Available

Last Activity: 2 Year ago(s)

question mark

Sum of series 2[n/2] ! [n/2]!/ n! [2Co-2C2+3C2....+[-1]^n[n+1]2Cn] where n is an even positive integer. Kindly provide solution of this question and how to generalise this. How do we know that which expansion will give this?

IIT JEE Entrance Exam

1 Answer Available

Last Activity: 2 Year ago(s)

question mark

I m foreigner,How much mark i need to get into IIT??

IIT JEE Entrance Exam

1 Answer Available

Last Activity: 2 Year ago(s)

View all Questions