 IIT JEE Entrance Exam> How to find common chord between parabola...
IIT JEE Entrance Exam> How to find common chord between parabola...

 1 Answers
1 Answers
Free trial
Last Activity: 8 Years ago
A collection of circles is called as a system or family of circles. There can be various types of family of circles
The general equation of a circle is x2 + y2 + 2gx + 2fy + c = 0. Since this equation involves three unknowns i.e. g, f and c so we need at least three conditions to get a unique circle.
For example, if we are given two circles and we want to determine the third circle touching both of them. We shall need one more condition. Without the condition we get the equation of family of circles which satisfies the two given conditions. Imposition of a third condition will result in the equation representing a particular circle.
Let us now see some of the ways of finding the family of circles when certain conditions are given:
1. Family of circles having a fixed centre
This equation is given by (x – h)2 + (y – k)2 = r2 (Figure given below) 
Since (h, k) is fixed, so the only parameter varying is r. This is one parameter family of circles, and is the equation of the family of concentric circles. Fixation of the radius will give a particular circle.
2. Equation of Family of circles passing through intersection of two circles S1=0 and S2=0.
The general equation of the family of circles passing through the intersection of S1 and S2 in given by S1 + kS2 = 0, where k? -1. Here again we have one-parameter (k) equation of family of circles. The particular value of the parameter gives a unique circle.
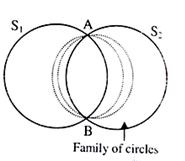
Caution:
If k = –1, we get equation of common chord i.e. straight line instead of circle.
Let S1= x2 + y2 + 2g1x + 2f1y + c1 = 0
S2 = x2 + y2 + 2g2x + 2f2y + c2= 0
Since, point lies on both the circles,
?xA2 + yA2 + 2g1xA + 2f1yA + c1 = 0
So, xA2 +yA2+ 2g2xA + 2f2yA + c2 = 0
? xA2 + yA2 + 2g1xA + 2f1yA + c1 + ? (xA2 + yA2 + 2g1 xA + 2f1yA + c1) = 0
? Point A(xA, yA) lies on S1 + ? S2 = 0 ? ? ? R
Similarly point B(xB, yB) lies on S1 + ? S2 = 0 ? ? ? R
? S1 + ? S2 = 0 is the family of circles through the intersection of S1 = 0 and S2 = 0.
3. Equation of a circle circumscribing a triangle whose sides are given by L1 = 0, L2 = 0, L3 = 0.
This equation is given by L1L2+?L2L3 + µL3 L1 = 0, provided coefficeint of xy = 0 and coefficient of x2 = coefficient of y2.
The particular value of the parameter ? and µ gives a unique circle.
4. Family of circles touching the circle S = 0 and line L = 0 at their point of contact
The required family is given by the equation S + ?L = 0, where ? is the required family.
5. Family of circle passing through two given points A(x1, x1) and B(x2, y2)
? Requiredfamily of circlesis 
6. Family of circles touching a given line L = 0 at a point (x1, y1) on the line is
(x – x1)2 + (y – y1)2 + ?L = 0, the particular value of the parameters ? gives a unique circle.
The equation of the family of circles which touch the line y – y1 = m (x – x1) at (x1, y1) for any values of m is (x – x1)2 + (y – y1)2 + ?[(y – y1) – m(x – x1)] = 0.
Here, we can have two sub-cases according as whether the line is parallel to x -axis or y-axis.
If this line through (x1, y1) is parallel to x-axis, then the equation of the family of circles touching it at (x1, y1) becomes (x – x1)2 + (y – y1)2 + K(y – y1) = 0.
And if the line through (x1, y1) is parallel to x-axis, then the equation of the family of circles touching it at (x1, y1) becomes (x – x1)2 + (y – y1)2 + K(y – y1) = 0.
7. Equation of circle circumscribing a quadrilateral whose sides in order are represented by the lines L1 = 0, L2 = 0, L3 = 0 and L4 = 0 .
The equation of the required family is given by L1L3 + ?L2L4 = 0, provided coefficient of x2= coefficient of y2 and coefficient of xy = 0.
Common chord of two circles
The line joining the points of intersection of two circles is called the common chord. If the equations of the circles are
S1 = x2 + y2 + 2g1x + 2f1y + c1 = 0
S2 = x2 + y2 + 2g2x + 2f2y + c2 = 0, then the equation of the common chord is S1 – S2 = 0.
Hence, the equation is 2x (g1- g2) + 2y (f1-f2) + c1 – c2 = 0.
Some key points:
-
The length of the common chord is 2v(r12 – p12) = 2v(r22 – p22), where p1 and p2 are the length of perpendicular drawn from the centre to the chord.
-
In the above equation of common chord, the coefficient of x2 and y2 in both the equations should be equal.
-
Two circles touch each other if the length of their common chord is zero.
-
The maximum length of the common chord is equal to the diameter of the smaller circle.
Angle of intersection of two circles:
The angle of intersection between two circles S = 0 ans S’ = 0 is deifned as the angle between their tangents at their point of intersection.
If S = x2 + y2 + 2g1x + 2f1y + c1 = 0
and S“ = x2 + y2 + 2g2x + 2f2y + c2 = 0, are two cricles with radii r1, r2 and ‘d’ is the distance between their centres then the angle of intersection? between them is given by
cos ? = (r12 + r22 – d2)/ 2r1r2 or cos ? = 2(g1g2 + f1f2) – (c1 + c2)/ 2v(g12 + f12 – c1) v(g22 + f22 – c2)
Note:
The two circles are said to intersect orthogonally if the angle of intersection of the circles i.e., the angle between their tangents at the point of intersection is 90°.
The condition for the two circles to cut each other orthogonally is 2gg1+ 2ff1 = c + c1 where (–g, –f) and (–g1, –f1) are the centres of the respective circles, S = 0 and S1 = 0.
When two circles intersect orthogonally then the length of the tangent of one circle from the centre of other circle is equal to the radius of the other circle.
External and Internal Contacts of Circles
A necessary and sufficient condition for the two circles to intersect at two distinct points is r1 + r2 > C1C2 >| r1 - r2|, where C1, C2 are the centres and r1, r2 be the radii of the two circles.
If two circles with centres C1(x1, y1) and C2(x2, y1) and radii r1 and r2 respectively, touch each other externally, C1C2 = r1 + r2. Coordinates of the point of contact are A = ((r1x2+r2x1)/(r1+r2),(r1y2+r2y1)/(r1+r2)).
The circles touch each other internally if C1C2 = r1 + r2.

The circles touch each other internally if C1C2 = r1 – r2.
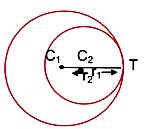
Coordinates of the point of contact are
T = ((r1x2 - r2x1)/(r1 - r2),(r1y2 - r2 y1)/(r1-r2)).
Illustration:
Examine whether the two circles x2 + y2 – 2x – 4y = 0 and x2 + y2 – 8y – 4 = 0 touch each other externally or internally.
Solution:
Let C1 and C2 be the centres of the circles.
? C1(1, 2) and C2(0, 4). Let r1 and r2 be the radii of the circles.
? r1 = v5 and r2 = 2v5. Also C1C2 = v(1 + 4)= v5.
But r1 + r2 = 3v5 and r2 – r1 = v5 = C1C2.
Hence the circles touch each other internally.
Illustration:
Find all the common tangents to the circles x2 + y2 – 2x – 6y + 9 = 0 and x2 + y2 – 6x – 2y + 1 = 0.
Solution:
The centres and the radii of the circles are
C1 (1, 3) and r1 = v(1 + 9 - 9) = 1, C2(–3, 1) and r2 = v(9 + 1 - 1) = 3,
C1C2 = v20, r1 + r2 = 4 = v16 and C1C2 > r1 + r2.
Sense the circles are non-intersecting. Thus there will be four common tangents.
Transverse common tangents are tangents drawn from the point P which divides C1C2 internally in the ratio 1 : 3.
Direct common tangents are tangents drawn from the point Q which divides C1C2 externally in the ratio 1 : 3.
Coordinates of P are ((1(-3)+3.1)/(1+3),(1.1+3.3)/(1+3)) i.e. (0,5/2) and coordinates of Q are (3, 4).
Transverse tangents are tangents through the point (0,5/2).
Any line through (0,5/2) is y – 5/2 = mx …… (1)
? mx – y + 5/2 = 0
Applying the usual condition of tangency to any of the circle, we get
(m.1 – 3 + 5/2 = 0)/v((m2+1) ) = 1 ? (m-1/2)2 = m2 + 1
? – m – 3/4 = 0 or 0.m2 – m – 3/4 = 0.
? m = –3/4 and 8 as coefficient of m2 is zero.
Therefore from (1),
(y-5/2)/x = m = 8 and -3/4 ? x = 0 is a tangent and 3x + 4y – 10 = 0 is another tangent.
Direct tangents are tangents drawn from the point Q(3, 4).
Now proceeding as for transverse tangents their equations are y = 4, 4x – 3y = 0.
Illustration:
Find the equation of the circle described on the common chord of the circles x2 + y2 – 4x – 5 = 0 and x2 + y2 + 8y+ 7 = 0 as diameter
Solution:
Equation of the common chord is S1 – S2 = 0
? x + 2y + 3 = 0
Equation of the circle through the two circles is S1 + ?S2 = 0
? x2 + y2 -4/(1+? ) x+8?y/(1+? )+(7? -5)/(1+? ) = 0.
Its centre (2/(1+? ),-4/(1+? )) lies on x + 2y + 3 = 0
? 2/(1+? )-8/(1+? ) + 3 = 0 ? 2 – 8? + 3 + 3? = 0 ? ? = 1.
Hence the required circle is x2 + y2 – 2x + 4y + 1 = 0.
Illustration:
The line Ax + By + C = 0 cuts the circle x2 + y2 + ax + by + c = 0 in P and Q. The Line A?x + B?y + C? = 0 cuts the circle x2 + y2 + a'x + b'y + c' = 0 in R and S. If P, Q, R, S are concyclic, prove that

Solution:
The equation of the circle through the first line and the first circle, i.e. through P and Q is
x2 + y2 + ax + by + c + ?1 (Ax + By + C) = 0. ........................ (1)
The equation of the circle through R and S is
x2 + y2 + a'x + b'y + c + ?2 (A'x + B'y + C') = 0.................... (2)
Since P, Q, R, S are concyclic, (1) and (2) are identical.
? 1 = (a+?1 A)/(a'+?2 A' )=(b+?1 B)/(b'+?2 B' )=(c+?1 C)/(c'+?2 C')
? ?1A-?2A' + a - a' = 0,
?1B -?2B' + b - b' = 0,
? 1C-? 2C' + c - c' = 0. 
Illustration:
Show that the circle passing through the origin and cutting the circles x2 + y2 - 2a1x - 2b1y + c = 0 and x2 + y2 - 2a2x - 2b2y + c = 0 orthogonally is

Solution:
Let the equation of the circle passing through the origin be
x2 + y2 + 2gx + 2fy = 0. ..................... (1)
It cuts the given two circles orthogonally
? -2ga1 - 2fb1 = c1 ? c1 + 2ga1 + 2fb1 = 0 ?2
and -2ga2 - 2fb2 = c2 ? c2 + 2ga2 + 2fb2 = 0 ? (3) 
Illustration:
Find the equation of the circle touching the line 2x + 3y + 1 = – at the point (1, -1) and is orthogonal to the circle which has the line segment having end points (0, -1) and (-2, 3) as the diameter.(IIT JEE 2004).
Solution:
The equation of the circle touching the line 2x + 3y + 1 = – at the point (1, -1) is
(x-1)2 + (y+1)2 + ?(2x + 3y + 1) = 0
This gives x2 + y2 + 2x(?-1) + y(3?+2) + (?+2) = 0 …. (1)
Now, this is orthogonal to the circle having end point of diameter (0, -1) and (-2, 3).
This yields x(x + 2) + (y + 1)(y - 3) = 0
i.e. x2 + y2 + 2x -2y -3 = 0
Hence, 2(? -2)/ 2. 1 + 2(3? + 2)/ 2 (-1) = ? + 2-3
This gives ? -3/2
hence, from equation (1), we have the equation of circle as 2x2 + 2y2 – 10x – 5y +1 =0.
Illustration:
Find a circle passing through the intersection of x2 + y2 - 4 = 0 and x2 + y2 - 6x + 5 = 0 which passes through the point (2, 1)?
Solution:
Family of required circles is S1 + ? S2 = 0
? (x2 + y2 - 4) + ? (x2 + y2 - 6x + 5) = 0
Since the required circle passes through the point (2, 1), the previous equation is satisfied for the point (2, 1)
? (4 + 1 - 4) + ? (4 + 1 - 12 + 5) = 0
1 - 2? = 0 ? ? =1/2
? Equation of the required circle is
(x2 + y2 - 4) + 1/2 (x2 + 2y - 6x + 5) = 0
? x2 + y2 - 2x - 1 = 0
Provide a better Answer & Earn Cool Goodies

LIVE ONLINE CLASSES
Prepraring for the competition made easy just by live online class.

Full Live Access

Study Material

Live Doubts Solving

Daily Class Assignments
Ask a Doubt
Get your questions answered by the expert for free
Other Related Questions on iit jee entrance exam

My rank is 29k, General, should I opt for any state college cse branch or some Nits in which in which I am getting ECE , chemical, mechanics etc....
iit jee entrance exam
Last Activity: 2 Years ago

How is Ranquer Eduzone,comparing, Akash,Fitjee,Resonance,Naryana
iit jee entrance exam
Last Activity: 2 Years ago

Can class 9th students study syllabus classof 11th
iit jee entrance exam
Last Activity: 2 Years ago


I m foreigner,How much mark i need to get into IIT??
iit jee entrance exam
Last Activity: 2 Years ago
