Samyak Jain
Last Activity: 6 Years ago
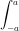 f(x) dx =
f(x) dx = 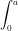 { f(x) + f(–x) } dx
{ f(x) + f(–x) } dxSo, given integral becomes
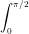 {1 / ( [x] + [sinx] + 4) + 1 / ( [–x] + [–sinx] + 4) } dx =
{1 / ( [x] + [sinx] + 4) + 1 / ( [–x] + [–sinx] + 4) } dx = 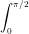 {1 / ( [x] + [sinx] + 4)} dx +
{1 / ( [x] + [sinx] + 4)} dx + 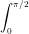 1 / ( [–x] + [–sinx] + 4) } dx
1 / ( [–x] + [–sinx] + 4) } dxLet us take first part of the integral.
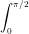 {1 / ( [x] + [sinx] + 4)} dx =
{1 / ( [x] + [sinx] + 4)} dx = 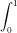 {1 / ( [x] + [sinx] + 4)} dx +
{1 / ( [x] + [sinx] + 4)} dx + 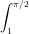 {1 / ( [x] + [sinx] + 4)} dx
{1 / ( [x] + [sinx] + 4)} dx = 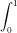 {1 / ( 0 + 0 + 4)} dx +
{1 / ( 0 + 0 + 4)} dx + 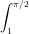 {1 / ( 1 + 0 + 4)} dx
{1 / ( 1 + 0 + 4)} dx 
for sinx belongs to (0,
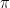
/2), [sinx] = 0 and x belongs to (0,1), x = 0 while x belongs to (1,
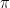
/2), x = 1.
= (1/4)(1 – 0) + (1/5)(
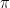
/2 – 1) =
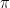
/10 + 1/4 – 1/5 =
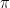
/10 + 1/20
=
(1/20)(2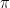 + 1)
+ 1) ….....(1)
Now,
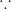 [x] + [–x] = –1
[x] + [–x] = –1 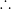 [–x] = –1 – [x] and [–sinx] = –1 – [sinx].
[–x] = –1 – [x] and [–sinx] = –1 – [sinx].[–x] + [–sinx] + 4 = –1 – [x] –1 – [sinx] + 4 = 2 – [x] – [sinx].
Take second part of the integral.
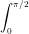 1 / ( [–x] + [–sinx] + 4) } dx =
1 / ( [–x] + [–sinx] + 4) } dx = 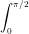 1 / ( 2 – [x] – [sinx]) } dx
1 / ( 2 – [x] – [sinx]) } dx = 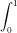 {1 / ( 2 – [x] – [sinx])} dx +
{1 / ( 2 – [x] – [sinx])} dx + 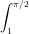 {1 / ( 2 – [x] – [sinx])} dx
{1 / ( 2 – [x] – [sinx])} dx = 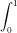 {1 / ( 2 – 0 – 0)} dx +
{1 / ( 2 – 0 – 0)} dx + 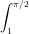 {1 / ( 2 – 1 – 0)} dx
{1 / ( 2 – 1 – 0)} dx [Reason is similar as above.]
= (1/2)(1 – 0) + (1/1)(
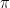
/2 – 1) = 1/2 +
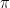
/2 – 1
=
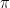
/2 – 1/2 =
(1/2)(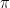 – 1)
– 1) …........(2)
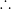
Given definite integral is : (1/20)(2
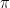
+ 1) + (1/2)(
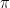
– 1) = (1/20)(2
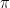
+ 1 + 10
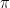
– 10)
= (1/20)(12
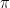
– 9)
=
(3/20)(4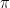 – 3) is the answer.
– 3) is the answer.




