Samyak Jain
Last Activity: 5 Years ago
Let speed of particle at t = 1s be u and that of particle at t = 2s be v.
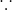
the graph is a straight line from t=0 to t=1, from t=1 to t=2 and t=2 to t=1, the motion is
uniformly accelerated in the three parts.
Average velocity is the ratio of total displacement to the time for which dispalcement has occured.
And for uniformly accelerated motion, we know, v = u + at ...(1) and v2 = u2 + 2as ...(2)
We need to calculate s/t. From (2), s = (v
2 – u
2)/2a
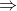
s/t = (v
2 – u
2)/2at
s/t = (v2 – u2)/2(v – u) = (v – u)(v + u)/2(v – u) = (u + v)/2,
i.e. the average velocity is the mean of initial and final velocities for uniformly accelerated motion.
(You can remember this as a result.)
So for the first part, average velocity = V1 = (0 + u) / 2 i.e. u = 2 V1.
Similarly, V
2 = (u + v)/2 = (2 V
1 + v) /2
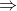
v = 2V
2 – 2V
1 v = 2(V2 – V1).
For last one second, average velocity = (v + 0)/2 = v/2 = 2(V2 – V1) / 2
= V2 – V1 .





