A uniform solid sphere is lying at rest between a vertical wall and a fixed inclined plane. There is no friction between sphere and wall. Coefficient of friction between sphere and fixed inclined plane is 1/2. What is the magnitude of frictional force? (Answer is zero, but how do you do the problem?)

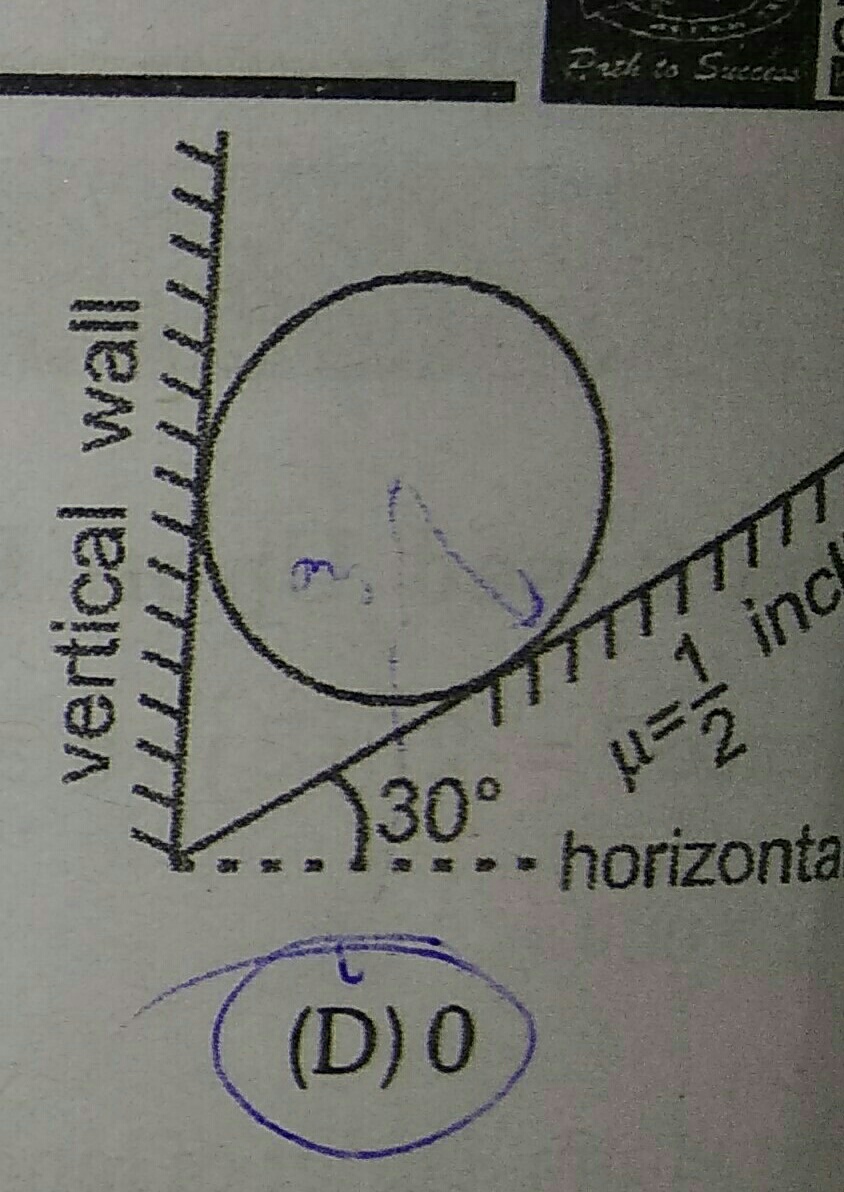
To tackle this problem, we need to analyze the forces acting on the sphere when it is positioned between the vertical wall and the inclined plane. The scenario indicates that the sphere is at rest, meaning that all forces acting on it are balanced. Let's break down the situation step by step.

Identifying the Forces

When the sphere is resting against the inclined plane and the wall, several forces come into play:

• Gravitational Force (Weight): This acts downward through the center of the sphere, equal to $mg$, where $m$ is the mass of the sphere and $g$ is the acceleration due to gravity.
• Normal Force from the Inclined Plane: This force acts perpendicular to the surface of the inclined plane. We'll denote it as $N$.
• Normal Force from the Wall: Since the wall is vertical, this force acts horizontally towards the sphere, denoted as $N_w$.
• Frictional Force: The frictional force can act to prevent the sphere from sliding down the inclined plane. In this case, we'll denote it as $f$.

Understanding the Equilibrium Condition

For the sphere to remain at rest, the sum of forces acting in both the vertical and horizontal directions must be zero. Let's analyze these forces:

Vertical Forces

The vertical forces acting on the sphere include the gravitational force and the vertical component of the normal force from the inclined plane. The vertical component of the normal force can be expressed as $N\sin (\theta )$, where $\theta$ is the angle of inclination. Therefore, the equilibrium condition in the vertical direction can be stated as:

$mg=N\sin (\theta )$

Horizontal Forces

In the horizontal direction, the normal force from the wall acts against the horizontal component of the normal force from the inclined plane. The horizontal component of the normal force can be expressed as $N\cos (\theta )$. Therefore, the equilibrium condition in the horizontal direction is:

$N_w=N\cos (\theta )$

Considering Friction

The frictional force, which opposes the motion of the sphere, depends on the normal force from the inclined plane. The maximum static frictional force can be calculated using the formula:

$f_{max}={\mu }_{s}N$

Where ${\mu }_s$ is the coefficient of static friction (given as $1/2$). However, for the frictional force to act, there must be a tendency for motion. In this case, since the sphere is at rest and there is no net force acting down the incline, the frictional force required to prevent any movement is actually zero.

Conclusion

Since there is no tendency for the sphere to slide down the inclined plane (because it is at rest), the frictional force acting on the sphere is zero. Therefore, even though we have a coefficient of friction, it does not come into play in this particular situation. The static friction force only arises when there is an attempt to move, which is not the case here. Hence, the magnitude of the frictional force is:

$f=0$

In summary, the concept hinges on the conditions of equilibrium and the absence of any force trying to move the sphere down the incline, leading to a frictional force of zero.