Shaswata Biswas
Last Activity: 9 Years ago
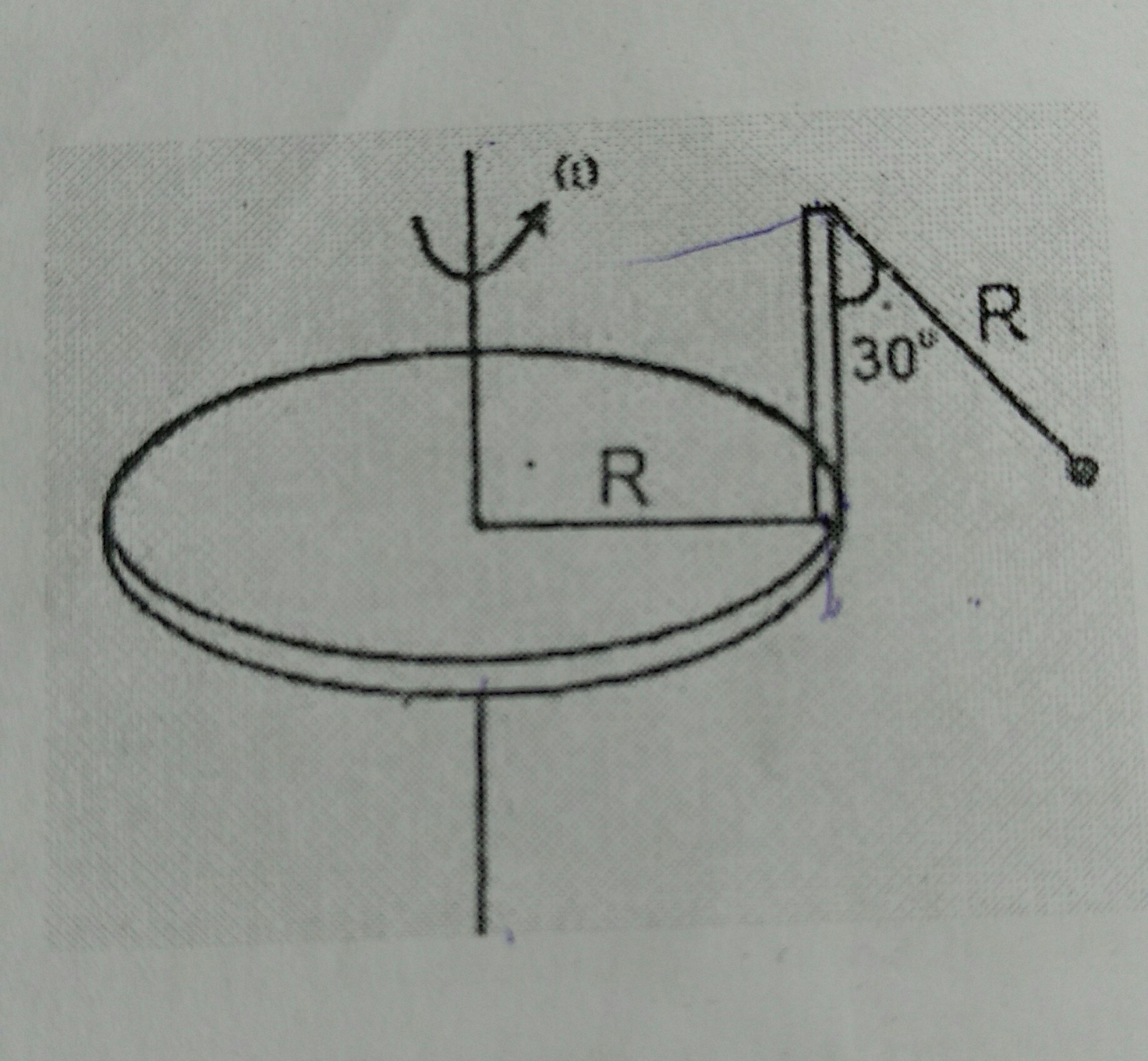
The ball suspended with a thread is scted upon by two forces : its weight mg, and tension in the string T. The resultant of these two forces produces the necessary centrepetal force along the horizontal so as to make the ball move along a cirular path of radius l (say).
Then, l = R + R.sin45
০ =
![R[\frac{1}{ \sqrt{2}} + 1]](http://latex.codecogs.com/gif.latex?R%5B%5Cfrac%7B1%7D%7B%20%5Csqrt%7B2%7D%7D%20+%201%5D)
And, on the ball :
- Weight of the ball mg acts vertically downwards
- Centrepetal force mw2l acts radially inward
- Tension acts along the string of pendulum.
Now,
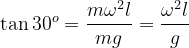
Or,
![\omega^{2} = \frac{gtan30^{o}}{l} = gtan30^{o} \div R[ \frac{1}{ \sqrt{2}} + 1]](http://latex.codecogs.com/gif.latex?%5Cdpi%7B120%7D%20%5Comega%5E%7B2%7D%20%3D%20%5Cfrac%7Bgtan30%5E%7Bo%7D%7D%7Bl%7D%20%3D%20gtan30%5E%7Bo%7D%20%5Cdiv%20R%5B%20%5Cfrac%7B1%7D%7B%20%5Csqrt%7B2%7D%7D%20+%201%5D)
So the required angular velocity,
![\omega = \sqrt{gtan30^{o} \div R[ \frac{1}{ \sqrt{2}} + 1]}](http://latex.codecogs.com/gif.latex?%5Cdpi%7B120%7D%20%5Comega%20%3D%20%5Csqrt%7Bgtan30%5E%7Bo%7D%20%5Cdiv%20R%5B%20%5Cfrac%7B1%7D%7B%20%5Csqrt%7B2%7D%7D%20+%201%5D%7D)
THANKS