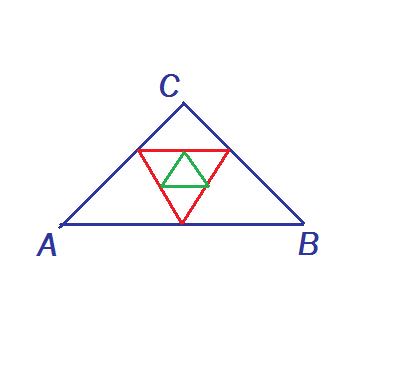
Q: As shown in figure ABC is an equilateral triangle with each side of resistance 'R'. Inside the triangle there are infinite no. of equilateral triangles each having resistance varying as R/2,R/4,R/6....of each side of respective triangles. Find the equivalent resistance between A and B.

The answer would be 2R since at every point they meet up effectively increasing the resistance so that any current wud only see the outer path when we think of infinite number of resistance.

How come 2R....not able to get it...plz explain.....thanx

At every point the resistors meet would be effectively increasing the tesistance. It is because any current here would only be able to see the outer path due to the presence of infinite number of triangular mesh. The outer path consists of two resistors with resistance of R each. They are in series and thus, the resultant resistance would be R+R = 2R. This is the effective resistance for such a complicated mesh.