Let Un=n!/(n+2)! , If Sn=summation n=1 to n Un then Lim n-->infinity Sn equals
Ajudiya Janvi , 7 Years ago
Grade 11
Differential Calculus> Let Un=n!/(n+2)! , If Sn=summation n=1 to...
2 AnswersNived
Last Activity: 5 Years ago
Un=1/(n+1)(n+2)=(n+2)–(n+2)/(n+1)(n+2)
=1/(n+1)–1/(n+2)
Sn =1/2–1/3+1/3–1/4.....+1/(n+1)–1/(n+2)
=1/2–1/(n+2)
Lim Sn = 1/2–lim 1/(n+2)
=1/2–0=1/2
Vikas TU
Last Activity: 5 Years ago
Dear student
We can say that , Un = n!/(n+2)!
So, by expanding this Un we get
Un = n!/(n+1)(n+2)n!
Cancel the n! ,term on both nimerator and denominator.
Un=1/(n+1)(n+2)=(n+2)–(n+2)/(n+1)(n+2)
=1/(n+1)–1/(n+2)
Sn =1/2–1/3+1/3–1/4.....+1/(n+1)–1/(n+2)
=1/2–1/(n+2)
Lim Sn = 1/2–lim 1/(n+2)
=1/2–0=1/2
Provide a better Answer & Earn Cool Goodies
Enter text here...
LIVE ONLINE CLASSES
Prepraring for the competition made easy just by live online class.
Full Live Access
Study Material
Live Doubts Solving
Daily Class Assignments
Ask a Doubt
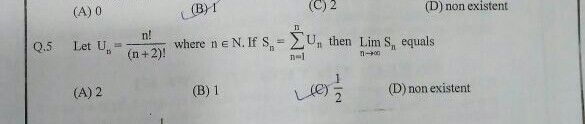
Get your questions answered by the expert for free
Enter text here...
Other Related Questions on differential calculus
the diameter of a roller is 84 cm and its length is 120 cm. it takes 500 complete revolution tomove once over to level a playground. find the area of the playground in square m?
differential calculus
1 Answer Available
Last Activity: 2 Years ago
Find dy/DX when y=x^sinx+sin-1√x. Please give me the solution of this problem.
differential calculus
0 Answer Available
Last Activity: 2 Years ago
If domain of f(x) is [-1, 2], then find the domain of f([x]-x^2+4), where [ ]denotes greatest integer function.
differential calculus
0 Answer Available
Last Activity: 2 Years ago
Solve the differential equation y’’+2ty’-4y=1, y(0)=y’(0)=0.
differential calculus
0 Answer Available
Last Activity: 2 Years ago
Example 20. (i) In a AABC, find the maxima and minima of u = sin A sin B sin Cwhere A + B + C = T(ii) In a plane triangle ABC, find the maximum value of cosA cosB cosC.
differential calculus
0 Answer Available
Last Activity: 2 Years ago