Image attached Show by LMVT and taking f(x) = log x that ( question attached in image)
Image attached
Show by LMVT and taking f(x) = log x that ( question attached in image)
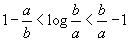

Last Activity: 2 Years ago

Last Activity: 2 Years ago

Last Activity: 2 Years ago

Last Activity: 3 Years ago

Last Activity: 3 Years ago