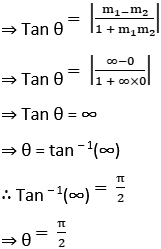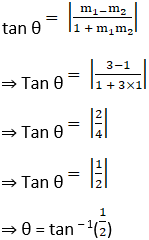0

Guest

Courses New

can you please solve this? (i) Find the angle of intersection of the curves 2y 2 = x 3 and y 2 = 32x. (Must figure) (ii) Find the angle of intersection of the curves x 2 = 4ay and 2y 2 = ax. (Must figure)

can you please solve this?
 (i) Find the angle of intersection of the curves 2y2 = x3 and y2 = 32x. (Must figure)                          
(ii) Find the angle of intersection of the curves x2 = 4ay and 2y2 = ax. (Must figure)                       

Question Image
Grade:12th pass

1 Answers

Harshit Singh
askIITians Faculty 5963 Points
3 years ago
Dear student

Solution to (i) query is given below:

Given as curve 2y2 = x3 ...(1)
and y2 = 32x ...(2)
First curve is 2y2 = x3
Differentiate with respect to x
4y.(dy/dx) = 3x2
m1 = dy/dx = 3x2/4y ...(3)
Second curve is y2 = 32x
2y.(dy/dx) = 32 y.
(dy/dx) = 16
m2 = dy/dx = 16/y ...(4)
Substitute (2) in (1)
2y2 = x3
2(32x) = x3
64x = x3
x3 - 64x = 0
x(x2 - 64) = 0
x = 0 & (x2 - 64) = 0
x = 0 & ±8
Substitutex = 0 & x = ±8 in (1) and (2),
y2= 32x
Now, when x = 0, y = 0
When x = 8 ⇒y2= 32 × 8
⇒y2= 256
⇒y = ±16
Substituteabove values for m1& m2,
Now, when x = 0, y = 16
m1 = dy/dx (3 x 02)/(4 x 8) = 0
When x = 8, y = 16
m1 = dy/dx = (3 x 82)/(4 x 16) = 3
The value of m1 is 0 & 3
Now, when x = 0, y = 0
m2 = dy/dx 1
6/y = 16/0 =∞
When y = 16
m2 = dy/dx
16/y = 16/16 = 1
The value of m2 is ∞ & 1 Now, when m1 = 0 & m2 =∞



699-621_1.png


Now, when m1 = 1/2 & m2 = 2
The angle of intersection of two curve is given by

699-2465_3.png

Thanks

Think You Can Provide A Better Answer ?

Other Related Questions on Differential Calculus

View all Questions »

ASK QUESTION

Get your questions answered by the expert for free

Answer and earn gift vouchers

Win Gift vouchers upto Rs 500/-

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Complete Self Study Package designed by Industry Leading Experts

Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child

Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Click Here Know More