Suppose two students at your school start a rumor. How could we describe the spread of the rumor throughout the school population? Could we determine a functionSsuch thatS(t)approximates the number of people that know the rumor at a time arbitrary timet,wheretis measured in, say, hours?
We'll begin by trying to decide what the graph ofSmight look like. Assume thatMis the population of your school and thatMis sufficiently large that it makes sense to model discrete numbers of students with a continuous function. Thus, ifS(3) = 127.8, we'll predict that the number of students who know the rumor after3hours is approximately128.
Study the six graphs below. For each graph, decide whether or not it could be the graph of the functionS. In each case, give the reasons for your decision.
Possible Graphs of S
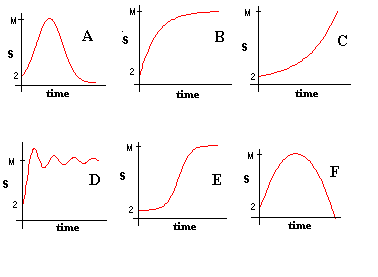
Describe three conditions that the graph ofSshould satisfy.
We could try to assemble a list of conditions that the graph ofSshould satisfy, i.e., conditions onSitself, hoping in this way to determine a model functionS. However, it will be easier to shift our attention todS/dt, the rate of change in the number of students who know the rumor -- the rate of spread of the rumor.
Describe three conditions thatdS/dt, the rate of spread of the rumor, should satisfy. Keep in mind that we are describing the rate of change of the number of students who know the rumor. Suppose for example, that you know the number of "rumor-aware" students at two o'clock. What factors might determine the number of rumor-aware students at three o'clock? Consider the nature of the rumor itself, conditions at your school, and at least one condition that changes as the rumor spreads.
Here are some possible factors you might have listed in Item 3.
How "juicy" the rumor is. The juicier the rumor the faster it will spread.
How many people know the rumor at the given time. The more that know the faster it spreads.
The average number of contacts a student makes with other students. The more contacts the faster the rumor spreads.
The number of students whodo notknow the rumor. Early on, almost everyone will be hearing the rumor for the first time. Later, after the rumor has had time to spread, many students will be reporting the rumor to those "already in the know." Even though the average number of contacts a student makes with other students remains constant, the rate of spread of the rumor begins to decrease because fewer students are hearing the rumor for the first time.
The factors listed are the ones we will consider in describingdS/dt. However, we could attempt take many other factors into consideration. List one or more factors different from the ones listed above that affect the rate of spread of the rumor.
We propose a symbolic descriptiondS/dtthat incorporates the conditions that we listed above -- but probably not the additional ones that you listed in Step 4:
dS/dt = k S (M - S).
HereMis the total number of students in the school andkis a constant that depends on both the juiciness of the rumor the average number of contacts between students. Remember that the symbolsSanddS/dtare not constants, but functions oft.
We assume thatkincreases with juiciness and with an increase in the average number of contacts. Thus, ifdS/dtsatisfies this relation, then the rate of spread of the rumor is greater for juicy rumors than it is for "dry" rumors and increases as the average number of contacts increases. So we have satisfied two of the four conditions listed above.
Explain why the relation
dS/dt = k S (M - S)
also incorporates our two additional conditions (restated below).
In what sense does the relation implythe more students know about the rumor the faster it spreads?
In what sense does the relation implythe rate of spread of the rumor decreases as the number of rumor-aware students increases?
This is our first example of adifferential equation. A differential equation is a relationship between a function, in our caseS, and the derivatives of the function. Our example
dS/dt = k S (M - S)
is called a "first-order differential equation" since it involves only the function and itsfirstderivative. On the other hand, the differential equation
d2Y/dt2+ dY/dt + Y = t
is asecond-orderdifferential equation.
Probably the differential equation
dS/dt = k S (M - S)
does not include all the factors you listed that control the rate of spread of the rumor. If you feel that a factor has been omitted, explain why, and rewrite the differential equation to include this factor.
According to our differential equation
dS/dt = k S (M - S),
under what circumstances will the rate of spread of the rumor will be0? ( There is more than one.)
If the units fordS/dtare students per hour, what units should be assign to the constantk?
Compare the rate at which the rumor spreads when1/4of the students know the rumor, i.e.,S = (1/4)M, to the rate when3/4know it. Is the rumor spreading faster when1/2of the students know the rumor or when3/4know the rumor?
What happens todS/dtasS(t)approachesM? Why is this reasonable?
Reconsider the possible graphs ofSpresented earlier.
Possible Graphs of S
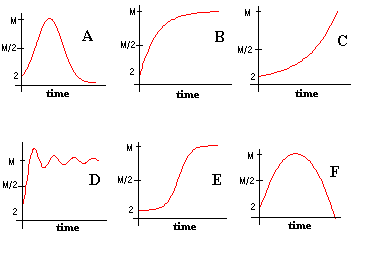
Ruchi
Askiitians Faculty