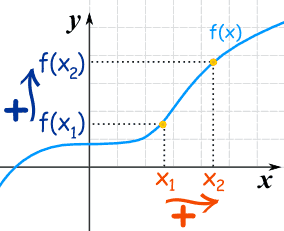
Dear Sir,

For the function f(x)=X^x . Find the points at which it is

1.Increasing.

2. Decreasing .

Hence Determine which of e^(pi) , (pi)^ e is greater .

Dear student,

Increasing Functions

A function is "increasing" if the y-value increases as the x-value increases, like this:

It is easy to see that y=f(x) tends to go up as it goes along.

What about that flat bit near the start? Is that OK?

• Yes, it is OK if you say the function is Increasing
• But it is not OK if you say the function is Strictly Increasing (no flatness allowed)

Using Algebra

What if you can't plot the graph to see if it is increasing? In that case is is good to have a definition using algebra.

For a function y=f(x):

That has to be true for any x₁, x₂, not just some nice ones you choose.

f(x) = x^x

d/dx [f(x)] = d/dx [ x^x ]

 f¹(x)       =x^x [ 1 + logx ]

f¹(x) = 0 , when 1+logx = 0 ,  x^x cannot be 0..

    1+ logx = 0

      logx = -1

        x = 1/e 

if x > 1/e , then function is increasing

if x < 1/e , then function is decreasing

increasing => (1/e , infinity)

decreasing=> (-infinity,1/e)