1800-150-456-789
FlagBACK
Flag Differential Calculus> L HOSPITAL RULE...
question mark

what is derivation of L hospital rule

vikash chandola , 14 Years ago
Grade
anser 1 Answers
SAGAR SINGH - IIT DELHI

Last Activity: 14 Years ago

Dear vikash,

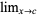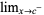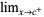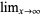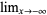Let lim stand for the limit lim_(x->c), lim_(x->c^-), lim_(x->c^+), lim_(x->infty), or lim_(x->-infty), and suppose that lim 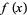f(x) and lim 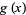g(x) are both zero or are both 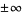+/-infty. If

lim(f^'(x))/(g^'(x))

has a finite value or if the limit is 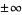+/-infty, then

lim(f(x))/(g(x))=lim(f^'(x))/(g^'(x)).

Historically, this result first appeared in l'Hospital's 1696 treatise, which was the first textbook on differential calculas. 

We are all IITians and here to help you in your IIT JEE preparation.

All the best.

 If you like this answer please approve it....

win exciting gifts by answering the questions on Discussion Forum

 

Sagar Singh

B.Tech IIT Delhi

Comes as a direct consequence of the Mean Value theorem. Useful for
computing limits of the formf(x)
g(x)wheref(x),g(x)→ 0. Connected to
limx→a
f?(x)
g?(x). Assumef (a) =g(a) = 0, and you want to compute limx→a
f(x)
g(x).

Use the mean value theorem to try to approximate the function. Asx ap- proachesa,f (x) should be approximatelyf (a) +f?(y)(x− a). Using the mean value theorem, we know such ay exists, sof (x) =f (a) +f?(y)(x− a) for somea < y < x. Likewise,g(x) =g(a) +g?(z)(x− a) for somea < z < x. So

f(x)
g(x)=f?(y)(x− a)
g?(z)(x− a)=f?(y)
g?(z)≈f?(x)
f?(y)
sincey andz approachx asx approachesa. Keep this idea in mind for the
proof.
2 Proof
Theorem (generalized mean value theorem): letf, g be continuous on [a, b],
and di?erentiable on (a, b). Then∃x ∈ (a, b) such thatf?(x)· (g(b)−g(a)) =
g?(x)(f(b)− f(a)).
Note: another way to think about this is that ifg?(x)?= 0, then
f?(x)
g?(x)=f(b)− f(a)
g(b)− g(a)

Provide a better Answer & Earn Cool Goodies

Enter text here...
star
LIVE ONLINE CLASSES

Prepraring for the competition made easy just by live online class.

tv

Full Live Access

material

Study Material

removal

Live Doubts Solving

assignment

Daily Class Assignments


Ask a Doubt

Get your questions answered by the expert for free

Enter text here...

Other Related Questions on differential calculus

question mark
the diameter of a roller is 84 cm and its length is 120 cm. it takes 500 complete revolution tomove once over to level a playground. find the area of the playground in square m?
differential calculus
1 Answer Available

Last Activity: 2 Years ago

question mark
Find dy/DX when y=x^sinx+sin-1√x. Please give me the solution of this problem.
differential calculus
0 Answer Available

Last Activity: 2 Years ago

question mark
If domain of f(x) is [-1, 2], then find the domain of f([x]-x^2+4), where [ ]denotes greatest integer function.
differential calculus
0 Answer Available

Last Activity: 2 Years ago

question mark
Solve the differential equation y’’+2ty’-4y=1, y(0)=y’(0)=0.
differential calculus
0 Answer Available

Last Activity: 2 Years ago

question mark
Example 20. (i) In a AABC, find the maxima and minima of u = sin A sin B sin Cwhere A + B + C = T(ii) In a plane triangle ABC, find the maximum value of cosA cosB cosC.
differential calculus
0 Answer Available

Last Activity: 2 Years ago