A circle cuts the parabola y2= 4ax in the points ( ati2, 2ati) for i = 1, 2, 3, 4. Prove that ti+ t2+ t3+ t4= O.
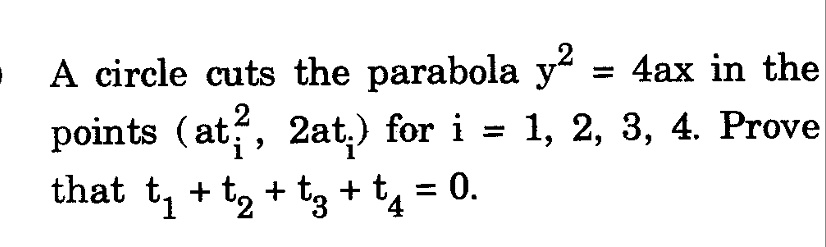
Get your questions answered by the expert for free

Last Activity: 2 Year ago(s)

Last Activity: 2 Year ago(s)

Last Activity: 2 Year ago(s)

Last Activity: 2 Year ago(s)

Last Activity: 2 Year ago(s)