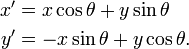0

Guest

Courses New

Line 'L' has interceps a and b on the coordinate axis. When the axis are rotated through a given angle, keeping the origin fixed, the same line 'L' has intercepts p and q on the new axis, then A) a 2 + b 2 = p 2 + q 2 B) a 2 + p 2 = b 2 + q 2 C) 1/a 2 + 1/b 2 = 1/p 2 + 1/q 2 D) 1/a 2 + 1/p 2 = 1/b 2 + 1/q 2

Line 'L' has interceps a and b on the coordinate axis. When the axis are rotated through a given angle, keeping the origin fixed, the same line 'L' has intercepts p and q on the new axis, then


A) a2 + b2 = p2 + q2


B) a2 + p2 = b2 + q2


C) 1/a2 + 1/b2 = 1/p2 + 1/q2


D) 1/a2 + 1/p2 = 1/b2 + 1/q2

Grade:12

4 Answers

Pratham Ashish
17 Points
13 years ago

hi,

 in the first coordinate sys,

x/a + y/b = 1     ..............................1

in other

x'/ p + y'/q  =1

where

 

\begin{align} x'&=x\cos\theta+y\sin\theta\\ y'&=-x\sin\theta+y\cos\theta. \end{align}

 

so,  x {  cos θ/p - sinθ /q }   + y { sinθ /p  + cosθ/ q }  =1 

comparing with (1).....

 {  cos θ/p - sinθ /q }/ 1/a   = { sinθ /p  + cosθ/ q }  / 1/b = 1/1

 cos θ/p - sinθ /q   = 1/a  ...............2

sinθ /p  + cosθ/ q  = 1/b ........................3

sq. and adding 2 &3

1/p^2 +  1/q^2  = 1/a^2 + 1/b^2

 

 

 

 

 

 

 

Aditya Lather
14 Points
4 years ago
H
Aditya Lather
14 Points
4 years ago
Here the length of perpendicular from origin to the lines would be equal hence on equating that distance we get
√(1/p^2 +1/q^2)=√(1/a^2+1/b^2)
On squaring both sides we get the answer
Kushagra Madhukar
askIITians Faculty 628 Points
2 years ago
Dear student,
Please find the answer to your question.
 
Here the length of perpendicular from origin to the lines would be equal hence on equating that distance we get
√(1/p^2 +1/q^2)=√(1/a^2+1/b^2)
On squaring both sides we get the answer
Hence the correct option will be C
 
Thanks and regards,
Kushagra

Think You Can Provide A Better Answer ?

Other Related Questions on Analytical Geometry

View all Questions »

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Complete Self Study Package designed by Industry Leading Experts

Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child

Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Click Here Know More