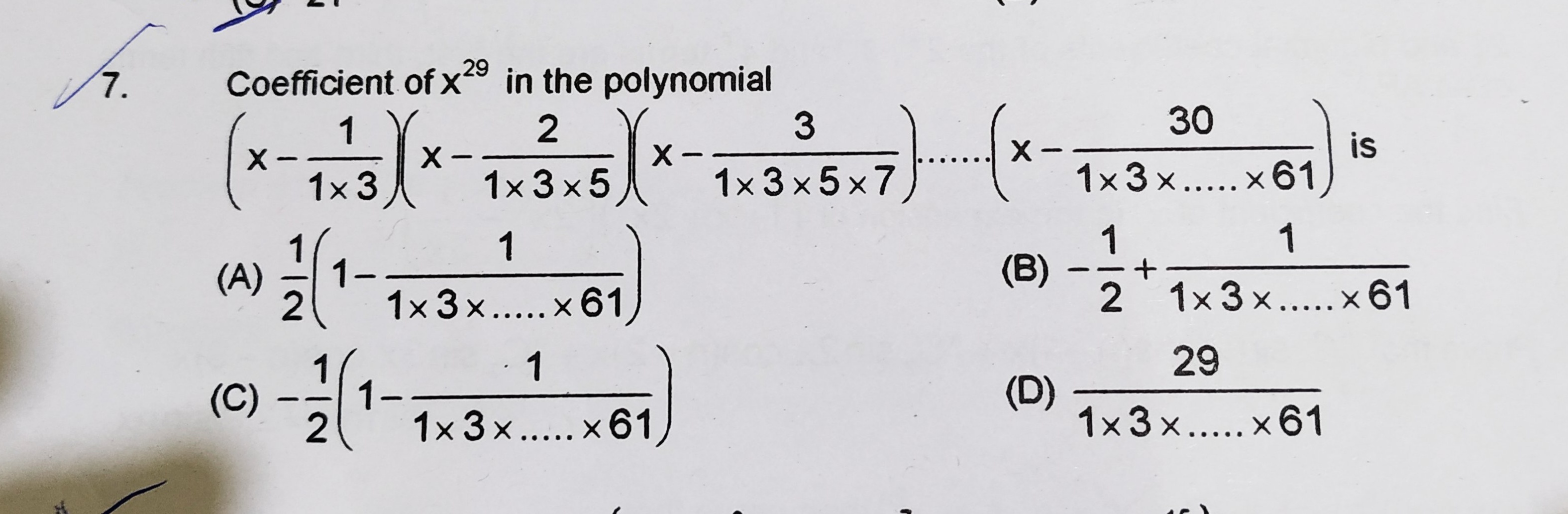Please answer to the question attached above from binomial theorem as soon as possible.

In total there are 30 terms multiplied to each other.

In order to get x^29 we have to choose 29 terms out of the 30 terms and multiply it with the constant of the term left. To get the coefficient x^29 we are all the constant term of the 30 terms

ie. -{(1/1*3)+(2/1*3*5)+...+(30/1*3*5...61)}

=(-1/2){(2/1*3)+(4/1*3*5)+...+(60/1*3*5...*61)}

=(-1/2){(3-1/1*3)+(5-1/1*3*5)+...+(61-1/1*3*5...*61)}

=(-1/2){1-(1/1*3)+(1/1*3)-(1/1*3*5)+....+(1/1*3*5...*59)-(1/1*3*5...*61)}

=(-1/2){1-(1/1*3*5*...*61)} 

So option C is correct. Please approve