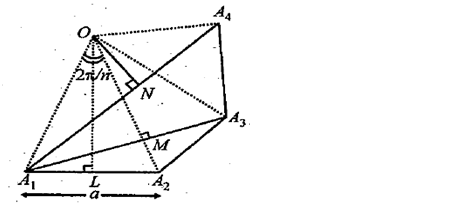
Let a be the side of n sided regular polygon
A1 A2 A3 A4 . . . . . . . . . . . . . . . . . . . An
∴ ∠ Subtended by each side at centre will be
= 2π/n
Let OL ⊥ A1 A2
Then ∠OLA1 = 90°, ∠A1 OL = π/n (∵ OA1 = OA2)
∴ In ∆OA1 L, sin A1 OL = A1 L/O A1
⇒ sin π/n = a/2 / O A1
⇒ O A1 = a/2 sin π/n . . . . . . . . . . . . . . . . . (1)
Again by geometry it can be proved that OM ⊥ A1 A3
In ∆ A1 M, sin 2π/n = A1 M/O A1
⇒ A1 M = OA1 sin 2π/n
⇒ A1 A3 = 2a sin 2π/n / 2 sin π/n [ Using eqn (1)]
Also if ON ⊥ A1 A4, then ON bisects angle
∠A1 OA4 = 3(2π/n)
∴ ∠A1 ON = 3 π/n
∴ In ∆ OA1 N, sin 3 π/2 = A1 N/O A1
⇒ A1 N = O A1 sin 3 π/h/n
⇒ A1 N4 = 2A1 N = 2a sin 3π/n / 2 sin π/n
But given that
1/A1 A2 = 1/A1 A3 + 1/A1 A4
⇒ 1/a = 1/a sin 2π/n / sin π/n + 1/a sin 3 π/n / sin π/n
⇒ sin 3π/n sin 2 π/n = (sin 3π/n + sin 2π/n) sin π/n
⇒ 2 sin 3π/n sin 2π/n = 2 sin 3 π/n + 2 sin 2 π/n sin π/n
⇒ cos π/n – cos 5 π/n = cos 2 π/n – cos 4 π/n + cos π/n – cos 3 π/n
⇒ cos 2 π/n + cos 5 π/n = cos 4 π/n + cos 3 π/n
⇒ 2 cos 7π/2n cos 3π/2n = 2 cos 7π/2n cos π/2n
⇒ cos 7π/2n (cos 3π/2n – cos π/2n) = 0
⇒ cos 7π/2n . 2 sin 2π/n sin π/n = 0
⇒ cos 7 π/2n = 0
Or sin 2π/n = 0 or sin π/n = 0
⇒ 7π/2n = (2k + 1) π/2 or 2π/n = k π/n or π/n = p π
⇒ n = 7/2k + 1 or n = 2/k or n = 1/k
But n should be a +ve integer being no. of sides and n ≥ 4 (four vertices being considered in the question)
∴ the only possibility is n = 7/2k + 1 for k = 0
∴ n = 7