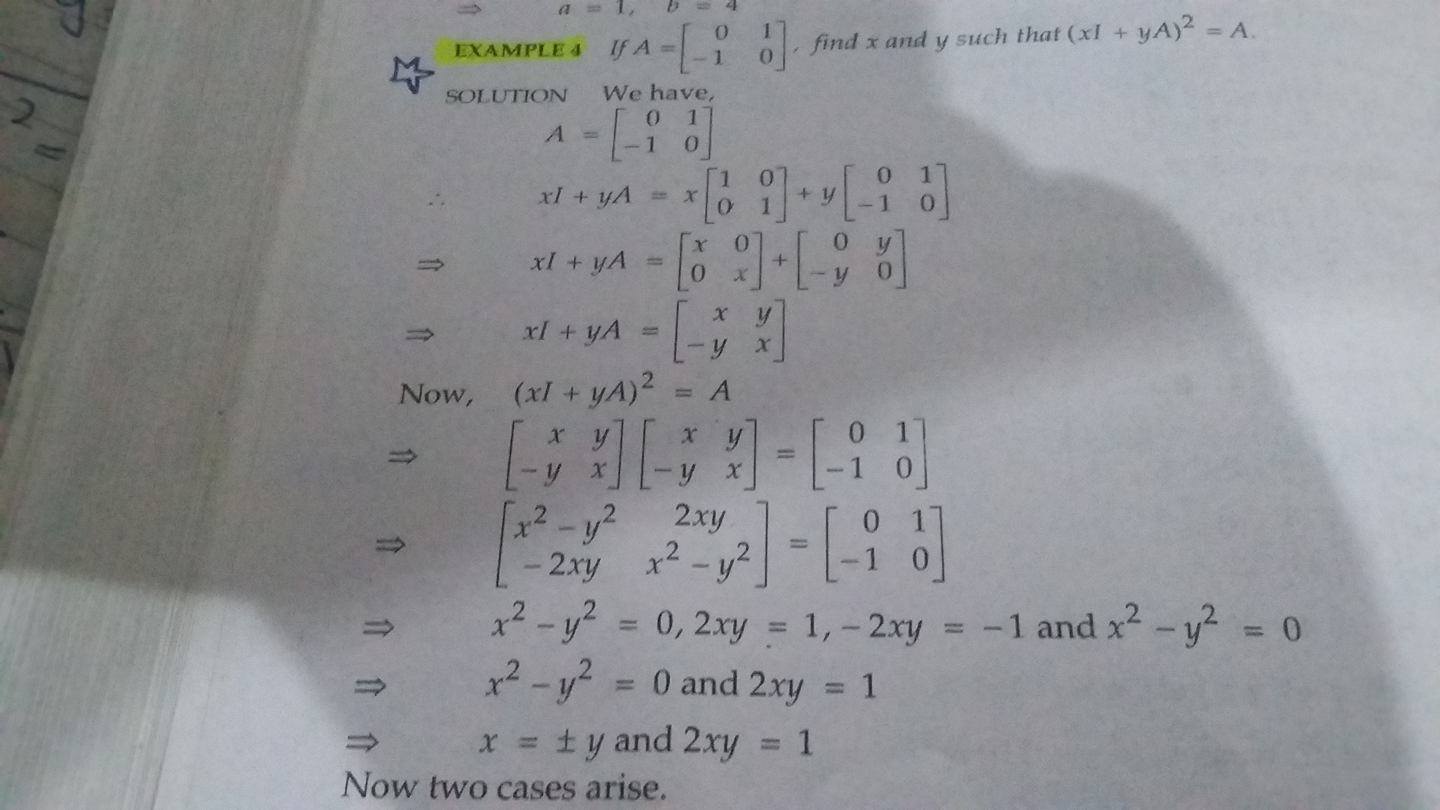Let's break down the equation \(x^2 - y^2 = 0\) step by step to clarify how we arrive at \(x = \pm y\) and why the signs are treated the way they are. This will help you understand the reasoning behind the algebraic manipulations involved.
Understanding the Equation
The equation \(x^2 - y^2 = 0\) can be factored using the difference of squares formula, which states that \(a^2 - b^2 = (a - b)(a + b)\). In our case, we can rewrite the equation as:
This means that either \(x - y = 0\) or \(x + y = 0\). Let's solve these two cases:
Case 1: \(x - y = 0\)
If \(x - y = 0\), then we can add \(y\) to both sides to get:
Case 2: \(x + y = 0\)
Combining the Results
From both cases, we see that \(x\) can equal \(y\) or \(x\) can equal \(-y\). This is where the notation \(x = \pm y\) comes from. It signifies that \(x\) can take on both positive and negative values of \(y\).
Addressing the Sign Confusion
Now, regarding your question about why we don't write \(+x = +y\) or similar variations: the notation \(x = \pm y\) is a concise way to express both possibilities in one statement. It implies:
- When \(y\) is positive, \(x\) can also be positive.
- When \(y\) is negative, \(x\) can also be negative.
In essence, the \(\pm\) symbol captures both scenarios without needing to explicitly state each one. This is a common practice in mathematics to simplify expressions and make them easier to read.
Conclusion
So, to summarize, when you start with \(x^2 - y^2 = 0\), you can factor it to find that \(x\) can equal either \(y\) or \(-y\). The notation \(x = \pm y\) effectively communicates that \(x\) can take on both positive and negative values of \(y\), which is why we don't need to specify the signs for \(x\) separately. I hope this clears up your confusion!