54x3 – 39x2 – 24x + 16 = 0 . Roots of this equation are in GP.
So let the roots be a/r , a , ar , where a/r is the first term and r is the common ratio of the GP.
Sum of roots = a/r + a + ar = – (–39) /54 = 39/54 ...(1)
Product of roots = (a/r)(a)(ar) = – (16) / 54
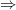
a
3 = – 16/54 = – 8/27
i.e. a3 = (– 2/3)3 or a = – 2/3
From (1), a(1/r + 1 + r) = 39/54
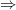
(– 2/3)(r
2 + r + 1)/r = 13/18.
(r
2 + r + 1)/r = – 13/12
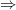
(r
2 + r + 1) = – (13/12)r or r
2 + (25/12)r + 1 = 0
12r2 + 25r + 12 = 0 i.e. 12r2 + 16r + 9r + 12 = 0 or (3r + 4)(4r + 3) = 0
r = – 4/3 or r = – 3/4
When r = – 4/3, a/r = (– 2/3)/(– 4/3) = 1/2 , a = – 2/3 , ar = (– 2/3)(– 4/3) = 8/9.
When r = – 3/4, a/r = (– 2/3)/(– 3/4) = 8/9 , a = – 2/3 , ar = (– 2/3)(– 3/4) = 1/2.
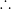
roots of the equation are
1/2 , – 2/3 , 8/9.





