Assume GP to be : a , ar , ar2 , …. , arn–1
So, sum of m terms of GP is Sm = a.(rm – 1) / (r – 1) …..(1)
Sm–1 = a.(rm–1 – 1) / (r – 1) …..(2)
Sum of products of m terms taken two at a time (say, M) can be calculated by using Bernoulli’s result, which is
n
2.

a
i a
j = (a
1 + a
2 + … + a
n)
2 – (a
12 + a
22 + … + a
n2) (= 2 times M in this problem)
i
Here a1, a2, … , an are terms of GP.
2 times M = Sm2 – (a2 + a2 r2 + … + a2 r2(m–1))
= [a.(rm – 1) / (r – 1)]2 – a2[1 + r2 + … + r2(m–1)]
= [a.(rm – 1) / (r – 1)]2 – a2[1.{(r2)m – 1} / (r2 – 1)]
[Note 1 + r2 + … + r2(m–1) is a GP with first term a and common ratio r2 and m number of terms]
2 M = [a.(rm – 1) / (r – 1)]2 – a2[{(rm)2 – 1} / (r2 – 1)]
= a2(rm – 1)2 / (r – 1)2 – a2(rm – 1)(rm + 1) / (r – 1)(r + 1) Take a2(rm – 1) / (r – 1) common.
= [ a2(rm – 1) / (r – 1) ] [ { (rm – 1) / (r – 1) } – { (rm + 1) / (r + 1) } ] Take LCM.
= [ a2(rm – 1) / (r – 1) ] [ { rm+1 + rm – r – 1 – rm+1 + rm – r + 1 } / (r – 1)(r + 1) ]
= [ a2(rm – 1) / (r – 1) ]. 2 . [ (rm – r) / (r – 1)(r + 1)]
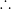
M = [ a
2(r
m – 1) / (r – 1) ] . r . (r
m – 1 – 1) / (r – 1)(r + 1) Separate a
2 as a . a
= r . { a.(rm – 1) / (r – 1) } { a.(rm – 1 – 1) / (r – 1)} / (r + 1)
= r . Sm . Sm–1 / (r + 1) From (1) & (2)
M = (r / (r + 1)) . Sm . Sm–1